問題來歷
據說著名猶太歷史學家 Josephus有過以下的故事:在羅馬人占領喬塔帕特後,39 個猶太人與Josephus及他的朋友躲到一個洞中,39個猶太人決定寧願死也不要被敵人抓到,於是決定了一個自殺方式,41個人排成一個圓圈,由第1個人開始報數,每報數到第3人該人就必須自殺,然後再由下一個重新報數,直到所有人都自殺身亡為止。然而Josephus 和他的朋友並不想遵從。首先從一個人開始,越過k-2個人(因為第一個人已經被越過),並殺掉第 k個人。接著,再越過k-1個人,並殺掉第 k個人。這個過程沿著圓圈一直進行,直到最終只剩下一個人留下,這個人就可以繼續活著。問題是,給定了和,一開始要站在什麼地方才能避免被處決?Josephus要他的朋友先假裝遵從,他將朋友與自己安排在第16個與第31個位置,於是逃過了這場死亡遊戲。
17世紀的法國數學家加斯帕在《數目的遊戲問題》中講了這樣一個故事:15個教徒和15 個非教徒在深海上遇險,必須將一半的人投入海中,其餘的人才能幸免於難,於是想了一個辦法:30個人圍成一圓圈,從第一個人開始依次報數,每數到第九個人就將他扔入大海,如此循環進行直到僅餘15個人為止。問怎樣排法,才能使每次投入大海的都是非教徒。
*問題分析與算法設計
約瑟夫問題並不難,但求解的方法很多;題目的變化形式也很多。這裡給出一種實現方法。
題目中30個人圍成一圈,因而啟發我們用一個循環的鏈來表示,可以使用結構數組來構成一個循環鏈。結構中有兩個成員,其一為指向下一個人的指針,以構成環形的鏈;其二為該人是否被扔下海的標記,為1表示還在船上。從第一個人開始對還未扔下海的人進行計數,每數到9時,將結構中的標記改為0,表示該人已被扔下海了。這樣循環計數直到有15個人被扔下海為止。
一般形式
約瑟夫問題是個有名的問題:N個人圍成一圈,從第一個開始報數,第M個將被殺掉,最後剩下一個,其餘人都將被殺掉。例如N=6,M=5,被殺掉的順序是:5,4,6,2,3,1。
分析:
(1)由於對於每個人只有死和活兩種狀態,因此可以用布朗型數組標記每個人的狀態,可用true表示死,false表示活。
(2)開始時每個人都是活的,所以數組初值全部賦為false。
(3)模擬殺人過程,直到所有人都被殺死為止。
pascal代碼1
C++代碼:
無論是用鍊表實現還是用數組實現都有一個共同點:要模擬整個遊戲過程,不僅程式寫起來比較煩,而且時間複雜度高達O(nm),當n,m非常大(例如上百萬,上千萬)的時候,幾乎是沒有辦法在短時間內出結果的。我們注意到原問題僅僅是要求出最後的勝利者的序號,而不是要讀者模擬整個過程。因此如果要追求效率,就要打破常規,實施一點數學策略。
為了討論方便,先把問題稍微改變一下,並不影響原意:
問題描述:n個人(編號0~(n-1)),從0開始報數,報到(m-1)的退出,剩下的人繼續從0開始報數。求勝利者的編號。
我們知道第一個人(編號一定是(m-1)) 出列之後,剩下的n-1個人組成了一個新的約瑟夫環(以編號為k=m mod n的人開始):
k k+1 k+2 ... n-2,n-1,0,1,2,... k-2
並且從k開始報0。
我們把他們的編號做一下轉換:
k --> 0
k+1 --> 1
k+2 --> 2
...
...
k-2 --> n-2
變換後就完完全全成為了(n-1)個人報數的子問題,假如我們知道這個子問題的解:例如x是最終的勝利者,那么根據上面這個表把這個x變回去不剛好就是n個人情況的解嗎?!!變回去的公式很簡單,相信大家都可以推出來:x'=(x+k) mod n
如何知道(n-1)個人報數的問題的解?對,只要知道(n-2)個人的解就行了。(n-2)個人的解呢?當然是先求(n-3)的情況 ---- 這顯然就是一個倒推問題!好了,思路出來了,下面寫遞推公式:
令f表示i個人玩遊戲報m退出最後勝利者的編號,最後的結果自然是f[n]
遞推公式
f[1]=0;
f[i]=(f[i-1]+m) mod i; (i>1)
有了這個公式,我們要做的就是從1-n順序算出f的數值,最後結果是f[n]。因為實際生活中編號總是從1開始,我們輸出f[n]+1
由於是逐級遞推,不需要保存每個f,程式也是異常簡單:
pascal代碼2
pascal代碼3
pascal代碼4
c++
pascal代碼5
這個算法的時間複雜度為O(n),相對於模擬算法已經有了很大的提高。算n,m等於一百萬,一千萬的情況不是問題了。可見,適當地運用數學策略,不僅可以讓編程變得簡單,而且往往會成倍地提高算法執行效率。
python代碼
該程式基於python3.x實現
約瑟夫問題10e100版(from vijios)
描述 Description
n個人排成一圈。從某個人開始,按順時針方向依次編號。從編號為1的人開始順時針“一二一”報數,報到2的人退出圈子。這樣不斷循環下去,圈子裡的人將不斷減少。由於人的個數是有限的,因此最終會剩下一個人。試問最後剩下的人最開始的編號。
輸入格式 Input Format
一個正整數n,表示人的個數。輸入數據保證數字n不超過100位。
輸出格式 Output Format
一個正整數。它表示經過“一二一”報數後最後剩下的人的編號。
樣例輸入 Sample Input
9
樣例輸出 Sample Output
3
時間限制 Time Limitation
各個測試點1s
注釋 Hint
樣例說明
當n=9時,退出圈子的人的編號依次為:
2 4 6 8 1 5 9 7
最後剩下的人編號為3
初見這道題,可能會想到模擬。可是數據實在太大啦!!
我們先拿手來算,可知n分別為1,2,3,4,5,6,7,8...時的結果是1,1,3,1,3,5,7,1...
有如下規律:從1到下一個1為一組,每一組中都是從1開始遞增的奇數,且每組元素的個數分別為1,2,4...
這樣就好弄了!!
大體思路如下:
①read(a)
②b:=1,c:=1{b為某一組的元素個數,c為累計所加到的數}
③while c<a do (b:=b*2,c:=b+c){超過目標時停止加數}
⑥c:=c-b{退到前一組}
⑦x:=a-c{算出目標為所在組的第幾個元素}
⑧ans:=x*2-1{求出該元素}
⑨write(ans)
有了思路,再加上高精度就可以了。我寫的代碼比較猥瑣,因為是先把上面的思路敲進去,再寫過程,又把一些簡單的過程合到主程式中了,所以有點亂,也有點猥瑣。起提供思路的作用還是完全可以的吧~~~
猴子選王
問題表述
一. 問題描述:
一堆猴子都有編號,編號是1,2,3 ...m,這群猴子(m個)按照1-m的順序圍坐一圈,從第1開始數,每數到第N個,該猴子就要離開此圈,這樣依次下來,直到圈中只剩下最後一隻猴子,則該猴子為大王。
約瑟夫
"密碼問題"
問題描述:編號為1、2、3、...、N的N個人按順時針方向圍坐一圈,每人持有一個密碼(正整數)。從指定
編號為1的人開始,按順時針方向自1開始順序報數,報到指定數M時停止報數,報M的人出列,並將
他的密碼作為新的M值,從他在順時針方向的下一個人開始,重新從1報數,依此類推,直至所有的
人全部出列為止。請設計一個程式求出出列的順序,其中N≤30,M及密碼值從鍵盤輸入。
二. 基本要求:
(1) 輸入數據:輸入m,n m,n 為整數,n<m
(2)中文提示按照m個猴子,數n 個數的方法,輸出為大王的猴子是幾號 ,建立一個函式來實現此功能
編程解決
•1.C程式
•C語言程式2
•C語言程式3: 用數組模擬鍊表
•pascal程式:
•c++程式
•約瑟夫數學算法
•約瑟夫遞推算法
•2、PHP模擬算法
php有非常完善的數據結構模擬方案,可以非常簡潔的解決這樣的問題!
3. Python遍歷數組
筆算解決
筆算解決約瑟夫問題
在M比較小的時候 ,可以用筆算的方法求解,
M=2
即N個人圍成一圈,1,2,1,2的報數,報到2就去死,直到只剩下一個人為止。
當N=2^k的時候,第一個報數的人就是最後一個死的,
對於任意的自然數N 都可以表示為N=2^k+t,其中t<n/2
於是當有t個人去死的時候,就只剩下2^k個人 ,這2^k個人中第一個報數的就是最後去死的。這2^k個人中第一個報數的人就是2t+1
於是就求出了當M=2時約瑟夫問題的解:
求出不大於N的最大的2的整數次冪,記為2^k,最後一個去死的人是2(N-2^k)+1
M=3
即N個人圍成一圈,1,2,3,1,2,3的報數,報到3就去死,直到只剩下一個人為止。
此時要比M=2時要複雜的多
我們以N=2009為例計算
N=2009,M=3時最後被殺死的人記為F(2009,3),或者可以簡單的記為F(2009)
假設這種情況下還剩下n個人,則下一輪將殺死[n/3]個人,[]表示小於等於這個數的最大整數,還剩下n-[n/3]個人
設這n個人為a1,a2,...,a(n-1),an
從a1開始報數,一圈之後,剩下的人為a1,a2,a4,a5,...a(n-n mod 3-1),a(n-n mod 3+1),..,an
於是可得:
1、這一輪中最後一個死的是a(n-n mod 3),下一輪第一個報數的是a(n-n mod 3+1)
2、若3|n,則最後死的人為新一輪的第F(n-[n/3])個人
若n mod 3≠0 且f(n-[n/3])<=n mod 3則最後死的人為新一輪的第n-[n/3]+F(n-[n/3])-(n mod 3)人
若n mod 3≠0 且f(n-[n/3])>n mod 3則最後死的人為新一輪的第F(n-[n/3])-(n mod 3)人
3、新一輪第k個人對應原來的第 3*[(k-1)/2]+(k-1)mod 2+1個人
綜合1,2,3可得:
F(1)=1,F(2)=2,F(3)=2,F(4)=1,F(5)=4,F(6)=1,
當f(n-[n/3])<=n mod 3時 k=n-[n/3]+F(n-[n/3])-(n mod 3),F(n)=3*[(k-1)/2]+(k-1)mod 2+1
當f(n-[n/3])>n mod 3時 k=F(n-[n/3])-(n mod 3) ,F(n)=3*[(k-1)/2]+(k-1)mod 2+1
這種算法需要計算 [log(3/2)2009]次 這個數不大於22,可以用筆算了
於是:
第一圈,將殺死669個人,這一圈最後一個被殺死的人是2007,還剩下1340個人,
第二圈,殺死446人,還剩下894人
第三圈,殺死298人,還剩下596人
第四圈,殺死198人,還剩下398人
第五圈,殺死132人,還剩下266人
第六圈,殺死88人,還剩下178人
第七圈,殺死59人,還剩下119人
第八圈,殺死39人,還剩下80人
第九圈,殺死26人,還剩下54人
第十圈,殺死18人,還剩36人
十一圈,殺死12人,還剩24人
十二圈,殺死8人,還剩16人
十三圈,殺死5人,還剩11人
十四圈,殺死3人,還剩8人
十五圈,殺死2人,還剩6人
F(1)=1,F(2)=2,F(3)=2,F(4)=1,F(5)=4,F(6)=1,
然後逆推回去
F(8)=7 F(11)=7 F(16)=8 f(24)=11 f(36)=16 f(54)=23 f(80)=31 f(119)=43 f(178)=62 f(266)=89 f(398)=130
F(596)=191 F(894)=286 F(1340)=425 F(2009)=634
規律解決
視頻中給出了經典的約瑟父問題的數學解法,當猴子選王問題的N=2時就是經典的約瑟父問題
對於經典約瑟父問題,視頻中的解法是:
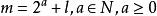 約瑟夫問題
約瑟夫問題 約瑟夫問題
約瑟夫問題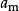 約瑟夫問題
約瑟夫問題1)找出令等式 成立的最大的 ,記為
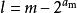 約瑟夫問題
約瑟夫問題2)求解出
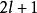 約瑟夫問題
約瑟夫問題3)所以,最後留下來的人的序號為
視頻中給出的解釋是:
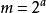 約瑟夫問題
約瑟夫問題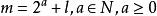 約瑟夫問題
約瑟夫問題 約瑟夫問題
約瑟夫問題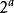 約瑟夫問題
約瑟夫問題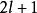 約瑟夫問題
約瑟夫問題 約瑟夫問題
約瑟夫問題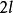 約瑟夫問題
約瑟夫問題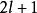 約瑟夫問題
約瑟夫問題當時,序號為1的人總是是最後留下來的人。對於,當去掉個人後,剩下的人正好組成個人圍成的圈,此圈中的序號1的人將是最後留下來的人。而對應到原來的圈,這個人的序號就是,因為去掉個人時正好就跳過了個人,而下一個人的序號就是。
推廣到猴子選王問題,從以上解法不難看出,解法就是把2換成N,即:
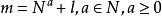 約瑟夫問題
約瑟夫問題 約瑟夫問題
約瑟夫問題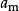 約瑟夫問題
約瑟夫問題1)找出令等式 成立的最大的 ,記為
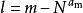 約瑟夫問題
約瑟夫問題2)求解出
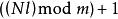 約瑟夫問題
約瑟夫問題3)所以,最後留下來的猴子的序號為 ,mod是取餘數,例如:3 mod 2 = 1
--------------------------
m=8, N=3,8=3^1+5, 按照他的算法,此時N=3,l=5, 按照他的算法最後剩下來的是8,事實上很容易直接驗算最後留下來的是7,上面的公式是錯誤的。

