背景
在控制系統的領域內，傳遞函式不僅可以表征線性時不變系統的動態特性，而且可以藉以研究系統的結構或參數變化對系統性能的影響。在經典控制理論中廣泛套用的頻率法和根軌跡法，就是在傳遞函式基礎上建立起來的。所以說，傳遞函式是經典控制理論中最基本也是最重要的概念。因此，傳遞函式的求取便具有十分重要的意義。
在控制系統傳遞函式的求解問題中，當給出了系統結構圖時，傳統的方法是通過對結構圖的等效變換與簡化，最終求解出系統的傳遞函式。當然，這種方法的好處是不言而喻的，它可以加深讀者對系統結構的了解。但同時，這種方法也具有不可克服的缺點c首先是它的繁瑣，每一步轉換都要畫出新的結構圖，不僅加大了工作量，而且在抄寫結構圖時，如果粗心抄錯一點，就會造成錯誤的傳遞，一誤再誤。其次，在簡化較複雜的結構圖時，很容易出錯，特別對於初學者來說，分析結構圖並不是很得心應手，因此會造成一些失誤而導致以後的錯誤。毋庸置言，傳統的求取傳遞函式的方法並不是很完善的。
基本概念
傳遞函式通常用於單輸入、單輸出的模擬電路，主要用在信號處理、通信理論、控制理論。這個術語經常專門用於如本文所述的線性時不變系統（LTI）。實際系統基本都有非線性的輸入輸出特性，但是許多系統在標稱參數範圍內的運行狀態非常接近於線性，所以實際套用中完全可以套用線性時不變系統理論表示其輸入輸出行為。有的書中也把其譯為：“轉移函式”。
對於最簡單的連續時間輸入信號x(t) 和輸出信號y(t) 來說，傳遞函式所反映的就是零狀態條件下輸入信號的拉普拉斯變換X(s) 與輸出信號的拉普拉斯變換Y(s) 之間的線性映射關係：
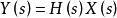系統傳遞函式或者
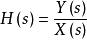系統傳遞函式其中 H(s) 就是此線性時不變系統的傳遞函式。
在離散時間系統中，套用Z變換，傳遞函式可以類似地表示成
基本釋義
系統傳遞函式把具有線性特性的對象的輸入與輸出間的關係，用一個函式（輸出波形的拉普拉斯變換與輸入波形的拉普拉斯變換之比）來表示的，稱為傳遞函式。原是控制工程學的用語，在生理學上往往用來表述心臟、呼吸器官、瞳孔等的特性。
系統的傳遞函式與描述其運動規律的微分方程是對應的。可根據組成系統各單元的傳遞函式和它們之間的聯結關係導出整體系統的傳遞函式，並用它分析系統的動態特性、穩定性，或根據給定要求綜合控制系統，設計滿意的控制器。以傳遞函式為工具分析和綜合控制系統的方法稱為頻域法。它不但是經典控制理論的基礎，而且在以時域方法為基礎的現代控制理論發展過程中，也不斷發展形成了多變數頻域控制理論，成為研究多變數控制系統的有力工具。傳遞函式中的復變數s在實部為零、虛部為角頻率時就是頻率回響。
傳遞函式也是《積分變換》里的概念。對復參數s，函式f(t)*e^(-st)在（-∞，+∞）的積分，稱為函式f(t)的（雙邊）拉普拉斯變換，簡稱拉氏變換（如果是在[0,+∞)內積分，則稱為單邊拉普拉斯變換，記作F(s)，這是個複變函數。
設一個系統的輸入函式為x(t），輸出函式為y(t)，則y(t)的拉氏變換Y(s)與x(t)的拉氏變換X(s)的商：W(s)=Y(s)/X(s)稱為這個系統的傳遞函式。
傳遞函式是由系統的本質特性確定的，與輸入量無關。知道傳遞函式以後，就可以由輸入量求輸出量，或者根據需要的輸出量確定輸入量了。
傳遞函式的概念在自動控制理論里有重要套用。
常識
傳遞函式概念的適用範圍限於線性常微分方程系統.當然，在這類系統的分析和設計中，傳遞函式方法的套用是很廣泛的。下面是有關傳遞函式的一些重要說明（下列各項說明中涉及的均為線性常微分方程描述的系統）：
1. 系統的傳遞函式是一種數學模型，它表示聯繫輸出變數與輸入變數的微分方程的一種運算方法；
2. 傳遞函式是系統本身的一種屬性，它與輸入量或驅動函式的大小和性質無關；
3. 傳遞函式包含聯繫輸入量與輸出量所必需的單位，但是它不提供有關係統物理結構的任何信息（許多物理上完全不同的系統，可以具有相同的傳遞函式，稱之為相似系統）；
4. 如果系統的傳遞函式已知，則可以針對各種不同形式的輸入量研究系統的輸出或回響，以便掌握系統的性質；
5. 如果不知道系統的傳遞函式，則可通過引入已知輸入量並研究系統輸出量的實驗方法，確定系統的傳遞函式.系統的傳遞函式一旦被確定，就能對系統的動態特性進行充分描述，它不同於對系統的物理描述；
6. 用傳遞函式表示的常用連續系統有兩種比較常用的數學模型。
性質
1、傳遞函式是一種數學模型，與系統的微分方程相對應。
2、是系統本身的一種屬性，與輸入量的大小和性質無關。
3、只適用於線性定常系統。
4、傳遞函式是單變數系統描述，外部描述。
5、傳遞函式是在零初始條件下定義的，不能反映在非零初始條件下系統的運動情況。
6、一般為復變數 S 的有理分式，即 n ≧ m。且所有的係數均為實數。
7、如果傳遞函式已知，則可針對各種不同形式的輸入量研究系統的輸出或回響。
8、如果傳遞函式未知，則可通過引入已知輸入量並研究系統輸出量的實驗方法，確定系統的傳遞函式。
9、傳遞函式與脈衝回響函式一一對應，脈衝回響函式是指系統在單位脈衝輸入量作用下的輸出。
極點和零點
系統傳遞函式 G( s)的特徵可由其極點和零點在 s複數平面上的分布來完全決定。用 D( s)代表 G( s)的分母多項式， M( s)代表 G( s)的分子多項式，則傳遞函式 G( s)的極點規定為特徵方程 D( s)=0的根，傳遞函式 G( s)的零點規定為方程 M( s)=0的根。極點（零點）的值可以是實數和複數，而當它們為複數時必以共軛對的形式出現，所以它們在 s複數平面上的分布必定是對稱於實數軸（橫軸）的。系統過渡過程的形態與其傳遞函式極點、零點（尤其是極點）的分布位置有密切的關係。
套用
傳遞函式主要套用在三個方面。
1、 確定系統的輸出回響。對於傳遞函式G(s)已知的系統，在輸入作用u(s)給定後，系統的輸出回響y(s)可直接由G(s)U(s)運用拉普拉斯反變換方法來定出。
2、分析系統參數變化對輸出回響的影響。對於閉環控制系統，運用根軌跡法可方便地分析系統開環增益的變化對閉環傳遞函式極點、零點位置的影響，從而可進一步估計對輸出回響的影響。
3、用於控制系統的設計。直接由系統開環傳遞函式進行設計時，採用根軌跡法。根據頻率回響來設計時，採用頻率回響法。
局限性
1960年以來關於能控性和能觀測性的研究表明，傳遞函式只是對系統內部結構的一種不完全的描述，只能表征其中直接或間接地由輸入可控制和從輸出中可觀測到的那一部分。引入狀態空間描述（見狀態空間法），可彌補這種缺陷。
