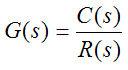傳遞函式定義
線上性定常系統中，當初始條件為零時，輸出量的拉普拉斯變換與輸入量的拉普拉斯變換之比。公式如右圖，其中C（s）、R（s)分別為輸出量和輸入量的拉普拉斯變換。
對於單變數系統，傳遞函式是以複數變數為自變數的一個標量函式；
對於多變數系統，輸入輸出關係的複數域表達式具有矩陣的形式，稱為傳遞函式矩陣，它的每一個元對應地是相應輸入和輸出間的傳遞函式。
引入傳遞函式，便有可能採用代數的方法或圖解分析的方法來簡化系統特性的確定和簡化控制系統的分析與綜合。傳遞函式是線性控制理論中最基本的概念之一，比其他形式的系統描述更為方便。
通過拉氏變換，可得傳遞函式的數學表達式為：
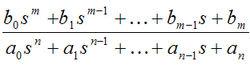傳遞函式的數學表達式其中 n ≧ m
傳遞函式性質
1、傳遞函式是一種數學模型，與系統的微分方程相對應。
2、是系統本身的一種屬性，與輸入量的大小和性質無關。
3、只適用於線性定常系統。
4、傳遞函式是單變數系統描述,外部描述。
5、傳遞函式是在零初始條件下定義的，不能反映在非零初始條件下系統的運動情況。
6、一般為復變數 S 的有理分式，即 n ≧ m。且所有的係數均為實數。
7、如果傳遞函式已知，則可針對各種不同形式的輸入量研究系統的輸出或回響。
8、如果傳遞函式未知，則可通過引入已知輸入量並研究系統輸出量的實驗方法，確定系統的傳遞函式。
9、傳遞函式與脈衝回響函式一一對應，脈衝回響函式是指系統在單位脈衝輸入量作用下的輸出。
微觀結構
線性定常系統的傳遞函式都是復變數 S 的有理分式，其分子多項式和分母多項式經分解後可寫如下形式：
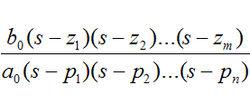因式分解後的傳遞函式傳遞函式零點
上面的多項式還可以表示為：
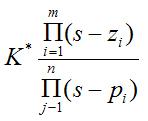另一種表示方法其中，Z i（i=1，2，......，m）是分子多項式等於零時的根，同時使G（s）= 0，故稱為傳遞函式的零點；
P i （j=1，2，......，n）是分母多項式等於零時的根，同時使G（s）=∞，故稱為傳遞函式的極點，又稱特徵根。
K* = b0/a0 稱為傳遞係數或根軌跡增益。
傳遞函式與它的零點、極點和傳遞係數一一對應。
零極點分布圖
在複數平面上表示傳遞函式的零點和極點的圖形，稱為傳遞函式的零極點分布圖。在圖中一般用”。“表示零點，用“X”表示極點。傳遞函式的零極點分布圖可以更形象地反映系統的全面特性。
