米迪定理

簡介

E·米迪在1836年證明了關於0.999…這類分數的一個一般的結果，現在稱為米迪定理。
米迪（Midy)定理說明若有質數p、少於p的正整數a、大於1的正整數b和任意正整數n，使得a/p在b進位制內的循環節長度是2n，且將這個分數用循環小數寫成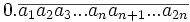則有以下結論：
ai+ai+n=b−1

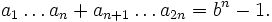
這個定理還可再作推廣（廣義米迪定理）：若k是l的正因子，則a1a2...ak+ak+1ak+2...a2k+...+al−k+1al−k+2...al是bk−1的倍數。

舉例

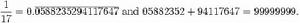
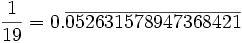
052631578+947368421=999999999
052631+578947+368421=999999


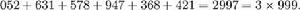
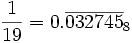
0328+7458=7778
038+278+458=778