相輔相成
算理與算法的關係
當學生進行了一定量的練習以後,發現了計算的規律:個位數只能與個位數直接相加、十位數只能與十位數直接相加、百位數只能與百位數直接相加,也就是相同數位上的數才能直接相加,最後再把幾個得數合併,這是學生感悟算理的過程;最後進行最佳化計算過程,為了便於計算一般寫成豎式形式,在此基礎上引導學生抽象概括出普遍適用的計算法則:把相同數位對齊列出豎式,再從個位加起,滿十向前一位進一,這就是算法。 從上面的分析可以看出算理與算法有這些關係:算理是客觀存在的規律,算法卻是人為規定的操作方法;算理為計算提供了正確的思維方式,保證了計算的合理性和正確性,算法為計算提供了快捷的操作方法,提高了計算的速度;算理是算法的理論依據,算法是算理的提煉和概括,算法必須以算理為前提,算理必須經過算法實現最佳化,它們是相輔相成的。
處理方法
如何處理算理和算法的關係
怎樣處理好算理與算法教學統一,使學生既理解算理,又能牢固掌握算法、提高計算的速度和正確率呢?下面就以二年級數學下冊70頁的兩位數乘一位數為例,說說如實現理算理與算法的的教學統一。
1、引導研究,理解算理
學生只有理解了計算的道理,才能“創造”出計算的方法,才能理解和掌握計算方法,才能正確迅速地計算,所以計算教學必須從算理開始。教學中要引導學生對計算的道理進行深入的研究,幫助學生套用已有的知識領悟計算的道理。首先引導學生思考:為什麼可以用14×2計算?使學生明白14×2表示求2個14是多少;其次,讓學生思考:你打算怎么計算14×2?使學生明白14是由1個十和4個一組成的,可以把14×2轉化成已經學過的乘法計算:先算2個10 是多少,再算2個4是多少,最後把兩次算的得數合併,計算的過程有三個算式:4×2=8,10×2=20,20+8=28。通過這樣的研究學生就理解兩位數乘一位數計算的道理,學生就能套用這樣的道理解決其他兩位數乘一位數的計算問題。
2、及時練習,鞏固內化
通過上面的計算研究,學生雖然理解了兩位數乘一位數的道理,但是此時學生對算理的理解還處於似懂非懂的狀態,學生是否真正掌握了算理還要經過實際計算才能得到檢驗和鞏固,此時及時組織學生進行相應的練習是很有必要的,只有在練習中才能把算理內化為自己的理解,才能使學生理解和掌握算理。所以在學生初步理解了算理後,應當及時組織學生用三個算式進行兩位數乘一位數的練習,使學生在練習中加深對算理的理解,在練習中牢固掌握算理,為後面的抽象、概括計算方法奠定堅實的基礎。
3、套用算理,進行創造
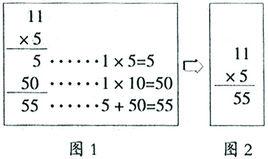
。算理是計算的思維本質,如果都這樣思考著算理進行計算,不但思維強度太大,而且計算的速度很慢算。為了提高計算的速度,使計算更方便、快捷,就必須尋找到計算的普遍規律,抽象、概括出計算法則。計算法則是算理的外在表達形式,是避開了複雜思維過程的程式化的操作步驟,它使計算變得簡便易行,它不但提高了計算的速度,還大大提高計算的正確率。所以當學生理解和掌握了算理之後,應引導學生對計算過程進行反思,啟發學生再思考:計算14×2要寫出三個算式,你的感覺怎樣?可以簡化一下嗎?怎么簡化?學生通過獨立思考、同伴交流創造方便、快捷的計算方法:可以像計算加減法那樣用豎式計算,根據算理:先算4×2=8,在個位上寫上8,再算10×2=20,在十位上寫2、個位上寫0,最後再把8和20加起來等於28,得出算理豎式。接著再啟發學生思考:還能再簡化嗎?通過師生共同研究,最終得出:加號可以省略,還可以把8個一與2個十直接合併,最佳化成簡化豎式。
4、觀察比較,歸納方法
當學生比較熟練地繼續豎式計算後,再引導學生對豎式計算過程進行觀察反思:這些乘法的豎式計算都是怎么算的?分幾個步驟?從而歸納出兩位數乘一位數的計算法則:先用一位乘數乘兩位數的個位數,積的末尾寫在個位上,再用一位乘數乘兩位的十位數,積的末尾寫在十位上。這時的計算就不再思考每一步的計算道理,只要按照這樣的操作步驟進行演算就能得到計算的結果,由於避開了複雜的思維過程,縮短計算的思維路徑,把計算演變成一種機械的、程式化的操作方法,所以計算的速度大大加快,計算的效率大大提高。
這樣的教學模式是以思維為主線、以算理為先導、以創造為契機,學生不但理解了算理,而且創造出了簡便的計算方法,並發現計算的規律,歸納出計算的法則,實現了算理與算法的統一。