基本介紹
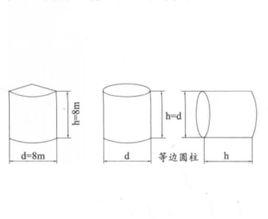
等邊圓柱是一個直圓柱，若其高與其底面直徑相等，則稱其為等邊圓柱。通過等邊圓柱旋轉軸的平面截圓柱，截面為正方形。
等邊圓柱等邊圓柱可內切一球，古希臘數學家阿基米德曾發現內切球的體積和表面積，都分別為圓柱體積及表面積的 ，阿基米德墓碑上就刻著圓柱容球圖，以資紀念 。
【例1】證明：表面積相等的正方體、等邊圓柱和球，它們的體積中，球的體積最大，等邊圓柱次之，正方體最小。
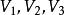等邊圓柱證明：設正方體、等邊圓柱和球的體積分別為 ，正方體棱長為a，等邊圓柱和球的半徑分別為r，R，
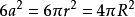等邊圓柱
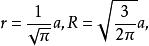等邊圓柱由它們的表面枳相等，可得 ，解得
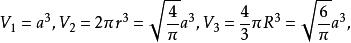等邊圓柱由幾何體體積公式可得
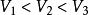等邊圓柱因此 ，球的體積最大，等邊圓柱次之，正方體最小。
規律：表面相同，越圓則容積越大 。
相關介紹
球的外切圓柱
如果一個球恰好能內容於一個等邊圓柱之中(即球與等邊圓柱的兩底面相切，球面與等邊圓柱的柱面交於一個球的大圓)，這個圓柱就叫這個球的外切圓柱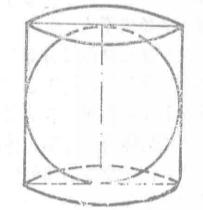(圖1) 。
圖1阿基米德的發現
雜草絲中，一座古墳，慕碑已經風化，字跡模糊不清。然而一個奇怪的標幟卻隱約地映人人們的眼帘：碑頂部刻著一個等邊圓柱以及它內切球的圖形。了解數學史的人很快就會知道，這裡長眠著古代最偉大的數學家阿基米德，已經有二千多年了 。
阿基米德(公元前287一前212年)在數學上的成就很多，其中他最感興趣的是關於球體積公式的推導，他為了找到球體積的計算方法，先用一個空心的等邊圓柱( 就是圓柱底面圓的直徑正好等於圓柱的高)的容器，裡面裝滿了水。然後把一個直徑等於這個圓柱高的球輕輕放進容器，再小心地把溢出的水收集起來，量出水的體積就是球的體積。他經過多次這樣的實驗，發現球的體積正好等於圓柱容積的2/3。假設圓柱底面半徑為R，我們不難用公式來驗算這個結論。圓柱的體積為
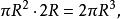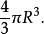等邊圓柱
等邊圓柱球的體積=
阿基米德非常重視這個發現，囑咐別人在他死後，能在他墓碑上刻上這個圖形。這就是，上面所提到的古墳墓碑上所刻的圖案。
阿基米德研究數學時聚精會神，可以說是廢寢忘食。冬天吃飯時，他常坐在火盆旁，一手端著飯碗，一手在火盆的灰燼里畫著幾何圖形，都忘了吃飯。
有一回， 因為一個數學問題沒解決，他埋頭鑽研，一直沒空去洗澡，身上很髒，發出一股難聞的氣味。家裡人硬把他推進浴室。那時候的人有個習慣，洗完澡後要在身上擦香油膏。阿基米德在浴室里洗了好半天都不見出來，家裡人感到很奇怪，在門外喊他也不見回音，便推門進去一看，原來他正坐在浴盆旁的凳子上，用手蘸著香油膏在皮膚上劃幾何圖形哩!他研究幾何圖形時，臉上總是笑呵呵的，嘴裡還嘰里咕嚕，家裡人說他像被神附了體一樣。
阿基米德為人謙遜，對待科學嚴肅慎重。他曾說過，他的一切發現別人都會發現，他毫不隱諱自己作品中的錯誤。他在自己所寫的《螺線論》這篇文章中，坦率地承認自己在以前的著作中所犯的某些錯誤，讓讀者從中吸取教訓。人們非常讚賞他這種高尚的品德。恩格斯誇獎他是對科學作了“ 精確而有系統研究’ 的代表人物之一。一位俄國數學家還在著作中寫下了讚美他的詩句:
這兒阿基米德出現了，
那古代的哲學家，
誰也不能和他相比擬，
他的功績全世界第一 。
儲油罐的設計原理
當你乘著輪船，沿著黃浦江航行，眺望兩岸時，就一定能見到許多盛有各種液體的貯油桶，它們高的幾十米，矮的也有近十米，大小雖不一樣，但看上去都顯得十分“勻稱”，既不“胖”，也不“瘦”。像這樣底面直徑和高恰好相等的圓柱體叫做等邊圓柱。
貯液桶一般常做成等邊圓柱。那么，它們為什麼不做成“胖”的或者“瘦”的，而要做成胖瘦適中，看上去很勻稱的等邊圓柱呢?這不僅是為了外形的美觀，更主要是為了節約造桶的材料。用數學語言來表達就是：在圓柱的容積V保持一定數值的情況下，圓柱體取什麼樣的形狀，它的全面積達到最小。我們已經通過計算證明等邊圓柱的全面積最小。
但我們應該注意，上面的結論只對有蓋的圓柱適用。如果無蓋的圓柱，做成等邊圓柱就不是最省料的了，而是應製成它的直徑等於高的二倍的圓柱，它的形狀看上去比較扁胖 。
