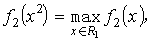等熵流動
正文
流體系統每一部分的熵在運動過程中都保持不變的一種流動。等熵流動要求每個流體質點的熵在流動過程中保持不變，即，
式中S為熵；v為速度；t為時間；為隨體導數;墷為梯度算符。在等熵流動中，雖然每個流體質點的熵保持不變，但不同流體質點的熵可以有不同的值，因而整個流場內的熵並非常數。如果流場在初始時刻是勻熵的（即各流體質點的熵相同），則等熵流動將使流場在任何時刻都是勻熵的,即S等於常數。有人把這種運動也稱為等熵流動。可逆的絕熱流動都是等熵流動，不可逆的絕熱流動則是不等熵的,由熱力學第二定律可知熵總是增加的,即。用熵表示的能量方程為：
，
式中ρ為密度；T為熱力學溫度；k為熱導率；ф為粘性耗損項。因此,要保持,必須使熱傳導項與粘性耗損項正好抵消，這在實際上是很難實現的。因此，有時把等熵流動和可逆的絕熱流動看成是等同的。從能量方程還可看出，忽略粘性和熱傳導的流體連續運動一定也是等熵流動。對於比熱為常數的完全氣體，熵表為：
，
式中 CV為定容比熱；為氣體比熱比,Cp為定壓比熱；p為壓力；C為常數。 從等熵方程 可得出。它同連續性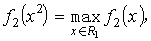方程
和運動方程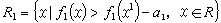
一起，構成了經典氣體動力學的封閉運動方程組。 參考書目
H.W.李普曼、A.羅什柯合著,時愛民等譯:《氣體動力學基礎》,機械工業出版社,北京,1981。(H.W.Liepmann and A.Roshko,Elements of Gasdynamics,John Wiley & Sons,New York,1957.)
