絕熱流動
正文
對整個流體介質而言，沒有熱量進出，而且流體內各部分之間沒有熱傳導的流動。熱量的進出可藉助於流體與周圍介質的熱傳導作用，也可以藉助於各種熱源來實現。介質的熱輻射，介質放電（電能轉化為熱），介質的化學反應（化學能轉化為熱）等，都可以看成是某種熱源。作絕熱流動的流體不存在上述現象。由於有粘性作用或有激波出現，流體介質會有機械能損耗，轉變為熱。這種現象雖也能使整個流體介質的熱量增加，但這種熱量不是自流體外部進入的，絕熱流動可以允許這種現象存在。對沒有這種機械能損耗的絕熱流動，通常稱為可逆絕熱流動。
嚴格的絕熱流動不允許有任何熱傳導現象存在。儘管實際的流體介質在溫度不均勻分布時總會或多或少要傳熱，只要熱傳導現象的影響不大，就可以忽略，把流體的流動看成是絕熱的。於是絕熱流動研究就具有實際意義。聲波和邊界層外的氣體動力學問題常被看作是絕熱流動。如空氣中聲波的運動，聯繫溫度和熱量變化的能量方程為：
，
式中ρ為密度;T為熱力學溫度;p為壓力;t為時間;k為熱導率;為定壓比熱；ф為粘性耗損項。若空氣中的聲波波長為λ，聲速為c，在上述能量方程中,慣性項的主要項是,其數量級大小為，而熱傳導項墷·(k墷T)的數量級為,慣性項與熱傳導項的量級之比為,用普朗特數Pr表示,則這兩者之比為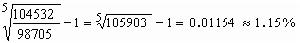
,其中μ為動力粘性係數。對空氣而言,Pr≈0.71,c=340米/秒，
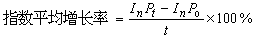=1.57×10-5米2/秒。人耳可聞的聲波波長一般在10-2～20米的範圍，若取λ為10-2米,則這個比值約為1.5×105。因此，熱傳導項的作用可以完全忽略不計，從而可以認為聲波運動是絕熱流動。 參考書目
H.W.李普曼、A.羅什柯合著,時愛民等譯:《氣體動力學基礎》,機械工業出版社,北京,1981。(H.W.Liepmann and A.Roshko,Elements of Gasdynamics，John Wiley ＆ Sons,New York,1957.)
