預備知識
線性空間
設 X 是一個非空集,K 是復(或實)數域,如果滿足條件:
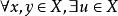 等價範數
等價範數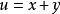 等價範數
等價範數 等價範數
等價範數(1)X 是一加法交換群,即對 ,記作 稱為 之和,適合
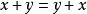 等價範數
等價範數① ;
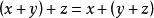 等價範數
等價範數② ;
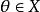 等價範數
等價範數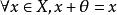 等價範數
等價範數③ 存在唯一的 ,對 ;
 等價範數
等價範數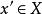 等價範數
等價範數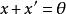 等價範數
等價範數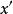 等價範數
等價範數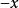 等價範數
等價範數④ 對任意的 ,存在唯一的 ,使得 ,記作 為 ;
 等價範數
等價範數 等價範數
等價範數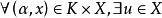 等價範數
等價範數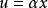 等價範數
等價範數 等價範數
等價範數 等價範數
等價範數(2)定義數域 K 中的數 與 的數乘運算,即 ,記作 稱為 對 的數乘,適合
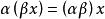 等價範數
等價範數① ;
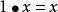 等價範數
等價範數② ;
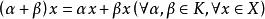 等價範數
等價範數③ ;
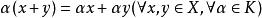 等價範數
等價範數④ ;
則稱 X 為一復(或實)線性空間。
線性空間範數
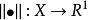 等價範數
等價範數若線性空間 X 上的一個非負值函式 滿足:
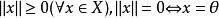 等價範數
等價範數(1)正定性: ;
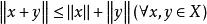 等價範數
等價範數(2)三角不等式: ;
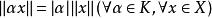 等價範數
等價範數(3)齊次性: ;
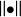 等價範數
等價範數則稱 為線性空間 X 上的一個範數。
賦范線性空間
當賦準範數的線性空間中的準範數是範數時,稱該空間為賦范線性空間。
相關比較
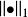 等價範數
等價範數 等價範數
等價範數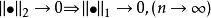 等價範數
等價範數 等價範數
等價範數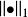 等價範數
等價範數設線上性空間 X 上給定了兩個範數 和 ,若有 ,則稱 比 強。
 等價範數
等價範數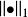 等價範數
等價範數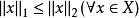 等價範數
等價範數為了 比 強,必須且只需存在常數 C>0 ,使得 。
定義
在許多分析問題中,引進範數或引進距離是為了研究一種收斂性。因此,如果我們關心的只是按照一定意義的收斂性而不是距離本身的大小,那么在空間上我們就可以認為決定同一收斂性的不同範數是等價的。等價範數是同一個線性空間上的兩個範數之間的一種關係。
數學表示
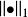 等價範數
等價範數 等價範數
等價範數 等價範數
等價範數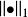 等價範數
等價範數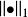 等價範數
等價範數 等價範數
等價範數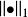 等價範數
等價範數 等價範數
等價範數設線上性空間 X 上給定了兩個範數 和 ,如果 比 強,並且 比 強,則稱 和 等價。
等價的意義
Banach空間中的兩範數等價,則說明這兩個範數的Banach空間拓撲性質相同,特別是 B 空間中序列的收斂性、集合的有界性、線性運算元的有界性、以及一族運算元的一致有界,在從一個範數變化到另一個範數時,都是不變的。
因此,與在同一個集合 X 上可以定義不同的距離使 X 成為不同的度量空間一樣,在同一個線性空間 E 上,也可以定義不同的範數,使E構成不同的賦范線性空間。
基本結論
結論1
(等價範數定理)
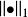 等價範數
等價範數 等價範數
等價範數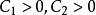 等價範數
等價範數設線上性空間 X 上給定了兩個範數 和 ,若存在兩個常數 ,使得
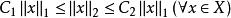 等價範數
等價範數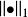 等價範數
等價範數 等價範數
等價範數則有兩範數 和 等價。
結論2
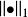 等價範數
等價範數 等價範數
等價範數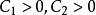 等價範數
等價範數設 X 是一個有窮維線性空間,若 和 都是 X 上的範數,則必有常數 ,使得:
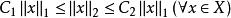 等價範數
等價範數該結論表明:具有相同維數的兩個有窮維線性賦范空間在代數上是同構的,在拓撲上是同胚的。

