第n級相變
正文
吉布斯函式 G對溫度T和壓力p的第n階偏導數開始變得不連續的相變。例如,通常的相變(如升華、氣化和熔融)是一級相變,因為在相變時,熵S和體積V都突然發生了一定的變化,S=-(дG/дT)p,V=(дG/дp)T,G的一階偏導數也突然發生了一定的變化,即G的一階偏導數是不連續的。有些相變中,S、V、T、p和G都保持不變,因此焓H、內能U 和亥姆霍茲函式A 也不變,但定壓熱容Cp則突然發生了一定數值的變化,而Cp/T=-д2G/дT2,即G的二階偏導數突然發生了一定數值的變化,而G的一階偏導數則連續,這樣的相變稱為二級相變。一級相變和二級相變時,各項熱力學性質隨溫度變化的情況如圖1所示,此圖中Tt為相變溫度。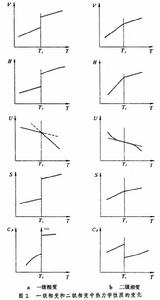 第n級相變
第n級相變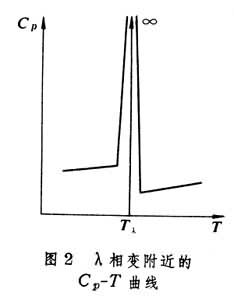 第n級相變
第n級相變今舉兩個λ相變的例子:①合金中的“有序-無序”的轉變;②在λ點的溫度、壓力下由通常的液氦 (即液氦Ⅰ)轉變為超流體氦(即液氦Ⅱ),λ點為 Tλ=2.177K,pλ=5.035kPa。
由圖1a可見,當溫度趨近於發生一級相變的溫度時,參與相變的兩個相中的任何一個相的Cp都保持著有限的數值,直至達到一級相變的溫度。只有當有少量的另一相存在時,Cp才變為無限大。在此以前,Cp並沒有表現出發生突然變化的任何先兆;而在圖2的曲線中,在發生λ相變時,雖然Cp也趨於無限大,但這些相變不是一級相變,因為Cp不是像一級相變中那樣突然變為無限大,而是在達到相變溫度以前,就已經隨著溫度的升高而較迅速地增大了。