定義
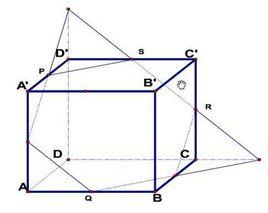
共面,又稱為共平面,是指幾何形狀在三維空間中落在同一平面上的關係。一般三個點必會共面,而四個點不一定會共面,兩條平行直線必共面。
性質
共面具有以下性質:
(1)三個不在一條直線上點必會共面;
(2)一條直線和這直線外一點必共面;
(3)兩條直線相交,則它們必共面;
(4)兩條平行直線必共面。
共麵條件
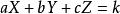 共面
共面如果這些點都在一條線上,那么肯定是共面的,所有通過這條線的平面都是結果;如果不都在一條線上,那么不在一條直線上的三個點可以確定一個平面,可以通過待定係數法求出一個平面方程: ,所有的點都滿足這個方程,就說明這些點共面。
點共面
公理1:如果一條直線的兩點在同一平面內,那么這條直線上的所有點都在這個平面內。(此時也稱直線在平面內或平面經過該直線。)
說明:公理1實質上給出了直線在平面內的定義,它給我們帶來了判斷直線在平面內的方法,同時也給出了直線在平面內的性質。即點A∈直線l,點B∈直線l,且點A∈平面α,點B∈平面α,則直線l 平面α。若直線l 平面α且P∈l,則P∈平面α。
公理2:如果兩個平面有一個公共點,則它們還有其他的公共點,這些公共點的集合是一條直線。
說明:公理2實質上給出了兩個平面相交的定義及兩個平面的交線的定義,也給出了兩個平面相交的性質。即:若兩個平面有一條公共的直線,則稱這兩個平面相交,這條直線叫做這兩個平面的交線。若兩個平面相交,則有且只有一條交線。利用公理2,可判定三點共線或三線共點.
公理3:經過不在同一條直線上的三點有且只有一個平面(即不共線的三點確定一個平面)。
推論1:經過一條直線和直線外一點有且只有一個平面。
推論2:經過兩條相交直線有且只有一個平面。
推論3:經過兩條平行線有且只有一個平面。
說明:若空間幾個點或直線都在同一平面內,我們就說它們共面。公理3及推論給了我們判定若干個元素(點、線)共面的方法。
共面直線
共面直線就是指代兩條或者多條直線同一個平面內,平行和相交的兩條或者多條直線就是共面直線。
直線共面的條件:
(1)兩條直線相交,他們共面;
(2)兩條直線平行,他們共面。
除上述兩種情況外的直線都可以判斷為兩條直線不共面。
共面向量定理
共面向量是一組有特殊位置關係的向量,即平行於同一個平面的一組向量、零向量與任何一組共面的向量共面,共面定理的定義為能平移到一個平面上的三個向量稱為共面向量。共面向量定理是數學學科的基本定理之一,屬於高中數學立體幾何的教學範疇,主要用於證明兩個向量共面,進而證明面面垂直等一系列複雜定理。
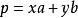 共面
共面共面定理得內容為:如果兩個向量a、b不共線,則向量p與向量a、b共面的充要條件是存在有序實數對(x,y),使 ,定義為:能平移到同一平面上的三個向量叫做共面向量。(即一個向量可以寫成另外兩個向量的線性組合)