定理定義
積分第一中值定理
積分第一中值定理
積分第一中值定理 積分第一中值定理 積分第一中值定理 積分第一中值定理 積分第一中值定理
積分第一中值定理如果函式 在閉區間 上連續， 在 上不變號，並且 在閉區間 上是可積的，則在 上至少存在一個點 ，使下式成立：
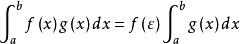積分第一中值定理定理證明
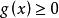積分第一中值定理 積分第一中值定理
積分第一中值定理 積分第一中值定理 積分第一中值定理 積分第一中值定理 積分第一中值定理
積分第一中值定理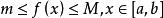
積分第一中值定理
積分第一中值定理 積分第一中值定理由於 在 上不變號，不妨設 。並且由 在 上的連續性可知， 在 上存在最大值 和最小值 ，使得 ，將不等式兩邊同時乘以 ，得到：
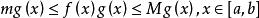積分第一中值定理 積分第一中值定理,對上式在上 取積分得
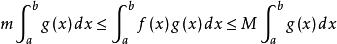積分第一中值定理
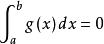積分第一中值定理
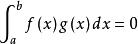積分第一中值定理若 ，上式等號成立， ，定理顯然成立。
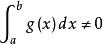積分第一中值定理
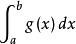積分第一中值定理若 ，不等式兩邊同除以 ，有
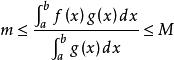積分第一中值定理
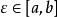積分第一中值定理
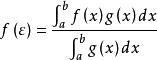積分第一中值定理 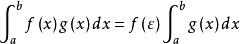積分第一中值定理由介值定理，存在 ，使得 ，即。定理得證。
套用實例
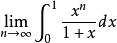積分第一中值定理求極限。
積分第一中值定理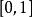
積分第一中值定理
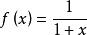積分第一中值定理
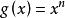積分第一中值定理
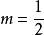積分第一中值定理
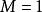積分第一中值定理解：取為，，，則，，並有
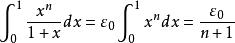積分第一中值定理
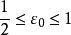積分第一中值定理由於有界，因此
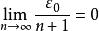積分第一中值定理即原式的極限為0。
