公式推導
柯西積分公式本身就是 柯西積分定理最直接、最重要的推論。利用我們所熟知的 柯西積分定理，
其證明過程是很簡潔的。在此不再贅述。
推論套用
柯西積分公式是一把鑰匙，他開啟了許多方法與定理，以下就是重要的幾個例子：
平均值定理
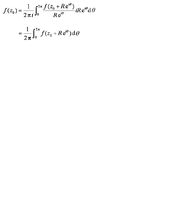柯西積分公式如果函式f（z）在圓│ξ-Zo│
解析函式無窮可微性
柯西積分公式一個解析函式不僅有一階導數, 而且有各高階導數, 它的 值也可用函式在邊界上的值通過積分來表示. 這一點和實變函式完全不同. 一個實變函式在某一區間上可導, 它的導數在這區間上是否連續也不一定, 更不要說它有高階導數存在了. 而利用柯西積分公式可以做數學歸納法證明如下定理：解析函式f(z)的導數仍為解析函式, 它的n階導數為:(見右圖) n！/ 2πi （ ∮c f（z）/（z-Zo）^(1+n) dz） 由定理可知，由函式在區域D內的 解析性，不僅推出其導數的連續性，而且也推出其各階導數在D記憶體在且連續。這是解析函式與一元實變數可微函式本質區別。這便是解析函式所具有的極好的性質,也使得人們對它的研究更具意義,讓解析函式論能夠單獨脫離於實函式而充滿活力!
柯西不等式
柯西積分公式其公式如右圖所示,它給出了一個很有用的估計導數的方法.
Liouville定理
有界整函式必為常數.利用柳維爾定理可以行反證法簡潔證明代數學基本定理:一元n次方程在複數域內必有解
Morera定理
即柯西積分定理的逆定理:(柯西積分定理:設C是一條簡單閉曲線，函式f（z）在以C為邊界的有界區域D內解析，在閉區域D‘上連續，那么有:f(z)對曲線的閉合積分值為零。)如果函式f(z)在區域D內連續，並且對於D內的任一條簡單閉曲線C，我們有∮c f(z) dz =0那么f(z)在區域D內解析。他刻畫了解析函式的又一種定義.
公式推廣
設C為任意簡單逐段光滑曲線,f(ξ)是在C上有定義的可積函式,則具有如下形式的積分稱為柯西型積分:
1 / 2πi （ ∮c f（ξ）/ξ-z dξ） z不屬於C
對於複變函數的研究頗具意義
