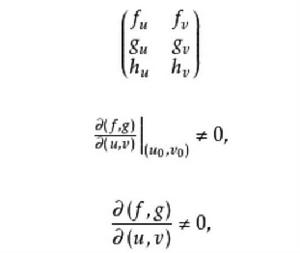秩定理

秩定理(rank theorem)是指映射的微分秩性質的一個定理，該定理斷言：設V與W分別是n維與m維C流形.f：V→W是一個C映射，且在每個點a∈V處df的秩是一個與a無關的整數r，則存在a與f(a)的區圖(U，φ)與(U′，φ′)，使得φ′°f°φ|φ(V)是映射(x₁，x₂，…，xn)↔(x₁，x₂，…，xr，0，…，0) 。

基本介紹

秩定理是有關雅可比矩陣的秩的一個定理，設f是從R 的區域A到R的區域B的連續可微函式，在每個x∈A處雅可比矩陣f′(x)的秩均為r，r≤m，r<n，則對每個x∈A，存在x的鄰域U⊆A，使點y∈f(U)的某n-r個坐標是另r個坐標的可微函式.例如：設m=2，n=3，F(u，v)=(x，y，z)=(f(u，v)，g(u，v)，h(u，v))，(u，v)∈A，F連續可微，(x，y，z)=(f(u，v)，g(u，v)，h(u，v))。若在(u，v)處，F的雅可比矩陣

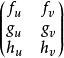秩定理

的秩為2，並且有

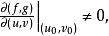秩定理

則在包含(u，v)的某個區域上

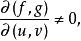秩定理

上述雅可比(Jacobi)矩陣的秩為2。由秩定理，在(x，y，z)的某鄰域內，F(A)中點的坐標(x，y，z)可表示為形如z=φ(x，y)。這就是說，以參數式x=f(u，v)，y=g(u，v)，z=h(u，v)表示的曲面，在對應於使

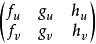秩定理

的秩為2的(u，v)的曲面上的點(x，y，z)附近，可以用z=φ(x，y)表示 。

相關概念及介紹

定義 設U是R 的開子集f:U→Rⁿ為C 映射，映射f的Jacobi矩陣在點x∈U的秩稱為映射f在x點的秩，若對每個x∈W(⊂U)，f的秩均為r，則稱f在W上的秩為r。

作映射f和一個微分同胚的複合，由於微分同胚有非奇異的Jacobi矩陣，根據鏈規則定理，這個複合映射的秩等於映射f的秩 。

定理1 （秩定理） 設G、H分別是R ，R 中的開集f:G→H是C 映射，且f在G上的秩等於r，如果點x∈G，y=f(x)∈H，則存在x,y的開鄰域G⊂G，H⊂H及R ，R 中的開集U、V和C 同胚

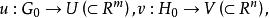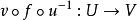秩定理

秩定理

使得映射具有下述簡單形式

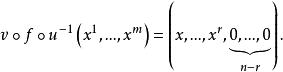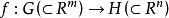秩定理

秩定理

注 秩定理告訴我們的是在定理1的條件下，即在G上的秩恆為某個常數r，則f在G上每點x的附近可通過局部C 同胚簡單表示為R 中的點在前r個坐標構成的r維坐標面上的投影。

推論 可用以下方式選取U和V：

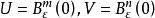秩定理

(i)或

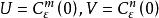秩定理

(ii)，此處

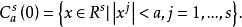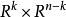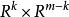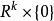秩定理

秩定理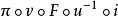

秩定理

秩定理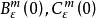

秩定理

秩定理

以π表示到R 的投影，i表示R 到的子集的單射，則在情況(i)，(ii)中，分別是上的恆同映射 。