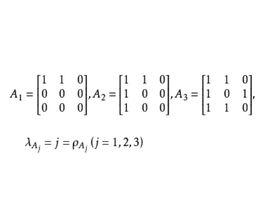基本概念
 項秩
項秩 項秩
項秩矩陣A的一行或一列統稱為A的一條線,一些線的集合稱為A的一個(線)覆蓋,如果這個集合中的線包含了A的所有非零元,A的線數最小的覆蓋稱為最小覆蓋,每個最小覆蓋中的線數稱為A的線秩(line rank)或覆蓋數,記為 ,顯然,A和B置換相抵 。
 項秩
項秩對偶地,A的一組兩兩不共線的非零元稱為一個無關元組;A的元素個數最大的無關元組稱為最大無關元組,每個最大無關元組中的元素個數稱為A的 項秩(term rank),記為 ,顯然,項秩也在置換相抵下不變。
【例1】記
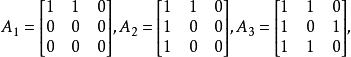 項秩
項秩 項秩
項秩則 ,其中A有兩個最大無關元組。
上例中矩陣的線秩與項秩相等並非偶然,這個結論對任一矩陣都成立。
相關性質定理
定理1(Frobenius-König) 設A是m×n矩陣,m≤n,則下列性質是互相等價的:
(1)A的項秩ρ<m;
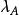 項秩
項秩(2)A的線秩<m;
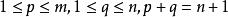 項秩
項秩(3)A含有p×q的零子矩陣,其中。
 項秩
項秩 項秩
項秩證(2) (3)是線秩定義的直接推論,現證(1) (3)。
情形1 m=n。
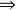 項秩
項秩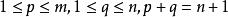 項秩
項秩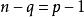 項秩
項秩 項秩
項秩 項秩
項秩(3) (1)。設A有一個p×q的零子矩陣.,則這個零子矩陣所在的p行至多只有個非零列,而如果=m,則在這ρ行中一定有A的最大無關元組中的p個元素,它們兩兩不共線,因此位於p個列上,這導致矛盾,所以<m。
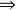 項秩
項秩 項秩
項秩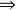 項秩
項秩 項秩
項秩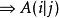 項秩
項秩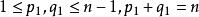 項秩
項秩(1) (3)。對n用歸納法論證,當n=1時,顯然成立,假沒結論對小於n階的方陣成立,現證對n階方陣A結論成立.若A是零方陣,(3)顯然成立,設A有非零元a,記A(i|j)為從A中划去第i和第j列後餘下的n-1階方陣,則有p₁×q₁的零子矩陣,。不妨設這個p₁×q₁的零子矩陣位於A的右上角,記
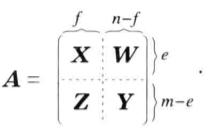 項秩
項秩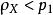 項秩
項秩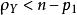 項秩
項秩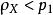 項秩
項秩 項秩
項秩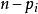 項秩
項秩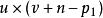 項秩
項秩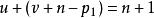 項秩
項秩由ρ<n,可知或,不妨設,根據歸納假設,p₁階方陣X一定有u×v的零子矩陣,這裡,A中這個u×v零子矩陣所在的u行和v列,連同A中最右端的列交匯所得的是一個的零子矩陣,其中,所以(3)對A成立 。
情形2 m<n。
令
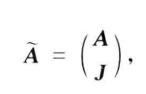 項秩
項秩 項秩
項秩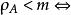 項秩
項秩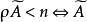 項秩
項秩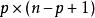 項秩
項秩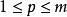 項秩
項秩 項秩
項秩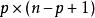 項秩
項秩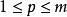 項秩
項秩這裡J是的全1矩陣,顯然 有的零子矩陣, A有零子矩陣,。
定理1的套用很多,下面只舉一例。
非負方陣A稱為是雙隨機的,如果A的每條線上的元素之和都是1。
定理2( Birkhoff) 設A是n階雙隨機方陣,則A可以表示為若干個n階置換方陣的凸線性組合,即
 項秩
項秩 項秩
項秩這裡諸P都是n階置換方陣, 是正數,
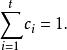 項秩
項秩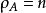 項秩
項秩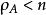 項秩
項秩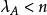 項秩
項秩證 先證,若,則由定理1可知,即可以用n-1條線覆蓋A的全部非零元,從而A的全部元素之和不超過n-1,這與A的全部元素之和應是n相矛盾。
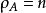 項秩
項秩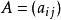 項秩
項秩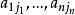 項秩
項秩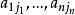 項秩
項秩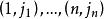 項秩
項秩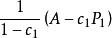 項秩
項秩現在對A的正元素的個數a用歸納法論證,顯然a≥n,且由a=n,知A是置換方陣,從而定理成立。當a>n時,,可知有由n個正元素組成的無關元組{ },記c₁=min{ },則0<c₁<1,令P是在n個位置, 處是1的n階置換方陣,則 是雙隨機方陣,但它的正元素個數少於A的正元素個數a,則由歸納假設可知
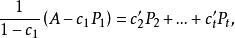 項秩
項秩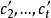 項秩
項秩 項秩
項秩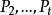 項秩
項秩這裡 >0, =1, 都是n階置換方陣,所以
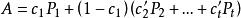 項秩
項秩即為所求。
推論1 設n階方陣A的元素是0或1,而且A的每條線上正好有k個1,則A一定可表為k個n階置換方陣的和。
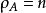 項秩
項秩證 和定理2一樣,可證,而A的一組n個無關的1確定了一個置換方陣P,對A-P,類似討論即得結論。
下面證明關於項秩和線秩的主要結果 :
定理3( König) 任一矩陣的項秩等於線秩。
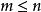 項秩
項秩 項秩
項秩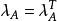 項秩
項秩證 設A是m×n矩陣。首先,可不妨設,否則,可以討論A的轉置A ,而易知ρ= , 。
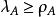 項秩
項秩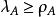 項秩
項秩直接從定義推得:在A的一個由λ條線組成的覆蓋中,必須含有A的ρ個無關元,但每條線中至多只能有這ρ個無關元中的一個,故
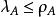 項秩
項秩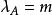 項秩
項秩 項秩
項秩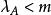 項秩
項秩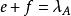 項秩
項秩現證。首先注意到,若,則由定理1可知,因此只要證明的情形,這時,設A有一個由e行和f列組成的覆蓋,,可不妨假設這是前e行和前f列,將A分塊成
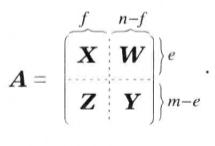 項秩
項秩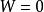 項秩
項秩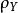 項秩
項秩易知,我們斷言=e。
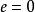 項秩
項秩 項秩
項秩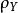 項秩
項秩若,則,從而=0。
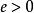 項秩
項秩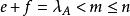 項秩
項秩 項秩
項秩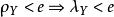 項秩
項秩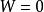 項秩
項秩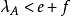 項秩
項秩若,則首先由,可知,從而根據定理1,,再由覆蓋的定義以及,可知,導致矛盾,從而斷言得證。
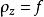 項秩
項秩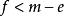 項秩
項秩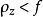 項秩
項秩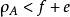 項秩
項秩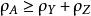 項秩
項秩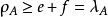 項秩
項秩同法可證,因,故由得,但顯然有,所以。