科學計算簡介
科學計算即是數值計算，科學計算是指套用計算機處理科學研究和工程技術中所遇到的數學計算。在現代科學和工程技術中，經常會遇到大量複雜的數學計算問題，這些問題用一般的計算工具來解決非常困難，而用計算機來處理卻非常容易。
自然科學規律通常用各種類型的數學方程式表達，科學計算的目的就是尋找這些方程式的數值解。這種計算涉及龐大的運算量，簡單的計算工具難以勝任。在計算機出現之前，科學研究和工程設計主要依靠實驗或試驗提供數據，計算僅處於輔助地位。計算機的迅速發展，使越來越多的複雜計算成為可能。利用計算機進行科學計算帶來了巨大的經濟效益，同時也使科學技術本身發生了根本變化：傳統的科學技術只包括理論和試驗兩個組成部分，使用計算機後，計算已成為同等重要的第三個組成部分。
計算過程
主要包括建立數學模型、建立求解的計算方法和計算機實現三個階段。
建立數學模型就是依據有關學科理論對所研究的對象確立一系列數量關係，即一套數學公式或方程式。複雜模型的合理簡化是避免運算量過大的重要措施。數學模型一般包含連續變數，如微分方程、積分方程。它們不能在數字計算機上直接處理。為此，先把問題離散化，即把問題化為包含有限個未知數的離散形式（如有限代數方程組），然後尋找求解方法。計算機實現包括編製程序、調試、運算和分析結果等一系列步驟。軟體技術的發展,為科學計算提供了合適的程式語言（如Fortran、ALGOL）和其他軟體工具,使工作效率和可靠性大為提高。
科學計算軟體
從70年代初期開始，逐漸出現了各種科學計算的軟體產品。它們基本上分為兩類：一類是面向數學問題的數學軟體，如求解線性代數方程組、常微分方程等;另一類是面向套用問題的工程套用軟體,如油田開發、飛機設計。
計算機的科學計算能力仍然有限，例如在天氣數值預報方面只能進行中、短期預報，在飛機氣動力設計方面只能分部件進行，在石油勘探方面只能處理粗糙的數學模型。為要進行長期的天氣數值預報、整體的飛機氣動力設計和在石油勘探中處理更精確的數學模型，都必須配備更強大的計算機。許多基礎學科和工程技術部門已提出超過現有計算能力的大型科學計算問題。這些問題的解決，有賴於兩方面的努力：一是創造出更高效的計算方法，一是大大提高計算機的速度。
作用
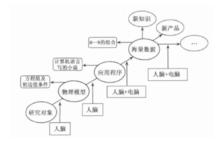科學計算流程什麼是科學計算? 粗略地說，科學計算是指利用計算機再現、預測和發現客觀世界運動規律和演化特性的全過程，包括建立物理模型，研究計算方法，設計並行算法，研製應用程式，開展模擬計算和分析計算結果等過程，圖1 是一幅表示科學計算過程的流程圖，用這個圖來說明作者對科學計算的理，要做科學計算。有了研究對象, 要針對其主要特徵，抓住主要矛盾，建立物理模型，所謂物理模型就是描述研究對象的一組方程以及約束方程組的初邊值條件，還有相應的物理參數，有了物理模型，需要採用與物理模型相適應的計算方法與算法，研製應用程式.所謂應用程式，形象一點說就是計算機語言編寫的小說。對於科學計算，經常使用的計算機語言有FO RT RAN 語言和C 語言。應用程式在計算機上進行運行，也就是利用計算機進行計算、求解方程組, 獲得方程組在特定約束條件下的解.與解析理論得到的方程或方程組的解不同，計算機求得的解不是一個表達式或一組表達式，而是一個數據集———海量數據集。有了數據， 需要對數據進行分析和評估，判斷結果的正確性, 發現新的現象, 總結新的規律, 認識新的機制, 再現和預測研究對象的運動規律和演化特性, 進而進行真實實驗或產品的理論設計, 產生新的知識、新的成果、新的生產力.我們經常聽到計算機仿真這個說法.實際上, 科學計算的本質不是仿真而是求真.在科學計算的流程中, 應用程式研製之前的工作主要依靠研究人員, 是“人腦”的事情.應用程式之後的工作不僅僅依靠研究人員, 還需要有計算機硬體作為基礎與前提, 是“人腦”加“電腦”的事情.高性能的計算機系統和數據分析處理系統是做好科學計算的必要條件, 是科學計算的重要組成部分.特別要強調的一點是, 對於科學計算來說, 電腦是不可或缺的, 但是只有充分發揮了人腦的作用, 才能最大限度地發揮電腦的作用, 才能做好科學計算,達到科學計算的根本目的.從流程圖1 的分析, 我們還可以看到, 科學計算需要物理、數學與計算機等方面人才的合作,需要多學科交叉融合.只有物理建模、計算方法、並行算法、程式研製和高性能計算機等方面有機結合,物理、數學與計算機等學科的人員真正融合, 才能做好科學計算。
地位
傳統的理論研究是以解析分析的方法為主, 它在科學原理與體系的建立過程中發揮了重要的作用, 並可以解決相對簡單的問題, 例如線性問題、平衡問題.但是, 隨著問題複雜性的增加, 理論研究的局限性也越來越明顯.很多問題, 如強非線性問題、非平衡問題、實際套用中發生的問題等, 傳統的理論研究已經無能為力.與理論研究相比, 科學計算不僅能夠處理線性問題、平衡問題, 更重要的是能夠處理強非線性問題、非平衡問題等, 能夠把科學的原理套用於解決更多、更複雜的實際問題 .科學計算經常也被稱為計算機虛擬實驗.與實驗研究相比, 科學計算至少有以下三個特點:一是無損傷.也就是說, 科學計算不會對環境等產生大的影響, 這一優點使得科學計算能夠承擔真實實驗不能完成的事, 例如要研究海嘯的破壞、地震的破壞、核爆炸的破壞，人類不可能進行真實實驗, 但可以進行科學計算, 進行計算機虛擬實驗.二是全過程、全時空診斷.真實的實驗, 無論用多少種方法、多少種儀器, 獲得的系統演化的信息是非常有限的, 難以做到全過程、全時空診斷.而全過程、全時空的信息對於人們認識、理解與控制研究對象極為關鍵.與真實實驗不同, 科學計算完成可以做到全過程、全時空診斷.只要在應用程式中加入相關的輸出程式, 在進行科學計算時, 研究人員就可以根據需要獲得任何一個時刻、任何一個地點研究對象發展和演化的全部信息, 使得研究人員可以充分了解和細緻認識研究對象的發展與演化，三是科學計算可以用相對低成本的方式, 短周期地反覆細緻地進行, 獲得各種條件下研究對象的全面、系統的信息。
發展建議
大力發展大規模科學計算的基礎算法
科學計算能力包括計算機硬體設備和套用軟體及支撐軟體的算法的能力。2005 年美國總統信息技術諮詢委員會報告指出：“儘管處理器性能的顯著增長廣為人知，然而改進算法和程式庫對於提高計算模擬能力的貢獻是如此之大，如同在硬體上的改進一樣。”以在科學計算套用中廣泛出現三維拉普拉斯方程計算求解為例，從上世紀50 年代的高斯消去法到80 年代的多重格線法，算法的改進使計算量從正比於格線數N的7/3 次方下降到最優的計算量正比於N，對於N等於100 萬，計算效率就改進1 億倍！2009 年出版的美國世界技術評估中心WTEC報告中對1998—2006 年獲著名超級計算Gorden Bell 獎的應用程式進行了評估，指出儘管獲獎程式的套用領域各不相同，但共同點是，算法（線性代數、圖剖分、區域分裂、高階離散）的進步使得獲Gorden Bell 獎應用程式對計算能力提高的貢獻超過摩爾定律。
當前科學計算所要解決的數值模擬問題往往非常複雜，給數值方法研究帶來了巨大的挑戰。數值方法研究目前面臨的突出共同難點表現為：高維數、計算規模大、多時空尺度、強非線性、不適定、長時間、奇異性、幾何複雜、高度病態、精度要求高等，並非有了高性能計算機就可以解決這些難點。數值模擬的困難常常表現為規模大得難以承受或失去時效；算法不收斂或誤差積累使結果面目全非；花費大量計算機時卻得不到結果或只得到錯誤結果；由於問題的奇異性使計算非正常中止；問題太複雜使算法難以實現等。這些難點問題近年來受到廣泛關注，已成為科學計算的研究熱點。
大力發展高性能科學計算套用軟體平台和框架
當前高性能計算機體系結構日趨複雜，CPU/GPU 異構、數千計算結點、結點內多處理器、處理器內多核、核內多功能部件及多級存儲是其顯著特點，對套用軟體的研製提出了挑戰。當前，我國科學計算套用軟體的研製面臨兩大瓶頸：第一，計算效率低，應用程式通常只能發揮數百處理器核峰值性能的10%以下；第二，研製周期長，與高性能計算機的快速發展不匹配。不突破這兩個瓶頸，我國並行套用軟體的研製就很難在總體上跟上高性能計算機的發展速度，無法將計算機技術的進步有效地用於科技創新，無法在國家重大套用領域發揮其應有的價值。
為了突破“計算效率低”和“研製周期長”兩大瓶頸，近年來我國科學工作者根據並行應用程式的多層軟體體系結構，提出了“集成共性、支撐個性”的新型並行軟體研製方法，在此新思路下，研製成功三維並行結構自適應軟體框架JASMIN 和三維並行自適應有限元軟體平台PHG，這兩個平台在基礎性共性算法（例如格線自適應和數百處理器核上的求解器）層次上對用戶禁止並行實現細節，並較好地解決了自適應並行實現中的負載平衡難題，在數10 萬億次國產並行計算機上，實現了高效並行計算。
在框架和平台的支撐下，各專業領域的科學計算研究人員可以集中於物理模型和計算方法的創新研究，無需了解並行計算的細節，就可以將新的物理模型和計算方法快速融入到大規模並行計算中，而計算機系統的研究人員，則可以集中於更高速度和更大規模計算機系統的研製，而無須顧及實現具體科學和工程計算的細節。
大力加強自主高性能計算科學軟體研製
高性能科學計算套用軟體的重要特點是多學科交叉，它是數學、物理、力學等基礎學科和相應套用學科及計算機軟體技術相結合而形成的以算法為核心，以計算機系統為支撐的知識密集型集成化信息產品，領域專業性非常強，只有建立高水平的多學科交叉研究隊伍，針對實際科學問題經過長時間的積累和沉澱，才能研製成功。
高水平的計算科學軟體需要先進的算法，我們建議在國家重大科技項目執行中能特別重視高性能計算科學軟體的自主研製，鼓勵更多的計算數學工作者深入科學計算中的瓶頸問題如材料計算、流體計算、電磁場計算、輻射流體力學計算、納米計算和生物計算中的算法研究、多尺度模型的分析與計算以及非平衡態的計算等，算法的創新要結合適合於計算的模型進行研究。
