地下水數學模擬
正文
把地下水現象和過程概化,用數學模型表達,求解所建立的模型以解決實際的水文地質問題的方法。地下水數學模擬一般分 3步進行。首先是建立模型。把實際的水文地質問題簡化,建立概念性模型,用一組數學表達式表達,得到所描述問題的數學模型。第二步是識別模型。模型建立以後,這一模型是否符合實際還是未知的,需要根據已有的實際資料進行校正,即把用模型計算的結果和實測資料進行對比,以修正模型並確定模型中有關的參數。最後是求解模型,得到所需的解答。地下水數學模型的分類 根據模型中變數的性質,把地下水數學模型分為確定性模型和隨機模型兩類。模型的變數之間能用確定性的函式關係描述的數學模型稱確定性模型,如描述地下水的水頭變化或地下水中溶質運移和熱量傳輸的數學模型。它們是以一個偏微分方程和一組初始條件和邊界條件構成的。把地下水現象當作隨機事件進行描述的數學模型稱隨機模型。模型中有一個或若干個變數為隨機變數,這種模型只能給出各變數之間非確定的、但有一定聯繫的相互關係。如回歸分析模型、時間序列模型等。隨機模型的建立只有當積累了長時間的觀測數據以後才有可能。
根據解決的問題,可把地下水數學模型分為模擬模型和最佳化模型兩類。模擬模型只描述地下水現象的物理過程,通常用於預報。如地下水的水頭模型、水質模型和水溫模型等,常用來預測地下水的水頭分布、溶質傳移和熱量傳輸。最佳化模型除了考慮物理過程以外,還要考慮社會的、經濟的、法律的各種非物理因素,尋求最佳方案,為決策提供依據。如地下水管理模型。
① 水頭模型 在均質、各向同性的承壓含水層中,地下水的二維穩定流動模型如下:
偏微分方程
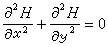
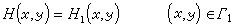
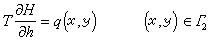
在非均質、各向同性的承壓含水層中,地下水二維非穩定流動模型如下:
偏微分方程
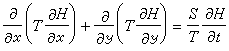
H(x,у,0)=H0(x,у)
邊界條件
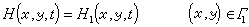
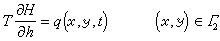
② 水溫模型 在無界的承壓含水層中,以定流量Q向單井中注入冷水時,含水層中水溫分布的數學模型如下:
偏微分方程
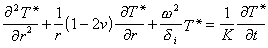
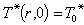
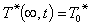
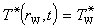
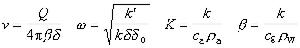
Q為注水量;T*為水溫;T奵為原來水溫;T奻為注入水的水溫;r為至抽水井中心的距離;δ為含水層的厚度;δi為不透水圈閉層的厚度;k為含水層的導熱率;k'為不透水圈閉層的導熱率;δo為不透水圈閉層傳熱帶的厚度;Ca為含水層的比熱;Cg為地下水的比熱;ρa為含水層的密度;ρw為水的密度。
③ 水質模型 地下水中的溶質一方面被水流挾帶隨水流動,稱為對流;另一方面在濃度差和微觀水流速度差的作用下,分布的範圍越來越大,稱為水動力彌散。當x軸方向和地下水流方向一致時,表示地下水中溶質運移的二維對流-彌散模型如下:
偏微分方程
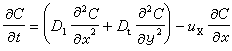
C(x,у,0)=C0(x,у) 邊界條件
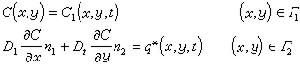
④ 管理模型 尋求在一定的允許降深、水量分配、環境保護和其他的約束條件下,使待開發地下水的成本最低或效益最高的方案,為決策提供依據。管理模型通常由一個目標函式和一組約束條件組成。一般為目標函式:
Z=c1x1+c2x2+…+…cnxn
取極大值(或極小值)。式中 xi(i=1,2,...,n)為決策變數,常為各水源的地下水開採量;c為價值係數,即單位體積水所產生的經濟效益(或開採單位體積水的成本)。並且滿足m個約束條件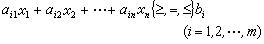
地下水數學模型的求解 求解數學模型的主要方法如下:①解析解法。求出滿足所給定的初始條件和邊界條件的偏微分方程的精確解。利用這個解可以求得任意時間和任意地點的水頭(或溶質濃度、或溫度)。但通常只有當含水層形狀規則(如無限含水層或有直線邊界的含水層),水文地質條件簡單時才有可能求得解析解。當條件複雜時常採用數值解。②數值解法。把計算區域和計算的時間離散化,求出區域內若干個點在某些時刻的水頭(或溶質濃度、或溫度)的近似解。常用的數值方法有:有限差分法,用差分方程近似代替微分方程求得近似解;有限單元法,把區域剖分為若干個單元,最常用的是三角形單元,對單元上的函式進行插值,一般用線性插值,求出各節點(即各個單元的公共頂點)上的水頭(或溶質濃度、或溫度)值;邊界單元法,只需將區域邊界剖分為單元,求出各節點的函式和函式的一階導數值,進而計算區域內部的水頭(或溶質濃度,或溫度)。數值解法需要利用電子計算機進行計算,用來求解複雜的、解析解難以解決的問題。③運籌學方法。管理模型要用運籌學的方法求解。主要用線性規劃、動態規劃、整數規劃和非線性規劃等方法。而以線性規劃最為常用,有時還需要將線性規劃和數值解法耦合求解。
參考書目
朱學愚、錢孝星、劉新仁著:《地下水資源評價》,南京大學出版社,南京,1987。
薛禹群、朱學愚著:《地下水動力學》,地質出版社,北京,1979。
J.Bear,hydraulics of Groundwater,McGraw-Hill,New York,1979.