礦物相律
正文
反映變質岩形成過程中達到熱力學多相平衡時,礦物相數與獨立組分數之間關係的法則。是吉布斯相律在封閉體系中的套用。由挪威科學家V.M.戈爾德施密特根據吉布斯相律於1911年提出的,又稱戈爾德施密特礦物相律。吉布斯相律是討論平衡體系內相數、獨立組分數和自由度三者之間關係的一般規律,即在平衡條件下,組分將最大限度地形成儘可能少的相。在一般情況下,影響體系平衡狀態的因素主要是溫度和壓力。所以吉布斯相律的一般表達式為
F=C +2-P
式中 F(自由度數)為體系中獨立可變的強度因素(溫度、壓力等)的數目。它們在一定範圍內可以任意改變而不會引起相的數目的改變。因此,自由度又稱為獨立變數。P(相數)為體系中平衡共生的相數。岩石學中,一種礦物為一個相,固溶體礦物也算一個相,如發生了固溶體分離,則主、客晶各為一個相。C(獨立組分數)為平衡體系中組成各相所需的最小數目的獨立物質。例如:
CaCO3+SiO2=CaSiO3+CO2↑
該平衡體系由4種物質來描述:CaCO3、SiO2、CaSiO3、CO2。但其獨立組分數是3而不是4。
戈爾德施密特認為,在變質地區內,變質礦物組合是按照變質帶分布的,每一個變質帶代表一定的溫度和壓力範圍,因此由變質反應形成的礦物組合是在溫度、壓力變化的條件下進行的(即 F=2)。所以相律的一般形式為
F=C +2-P=2
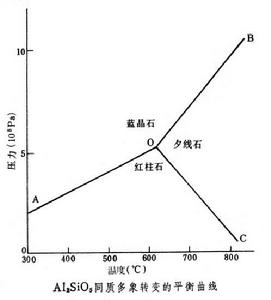
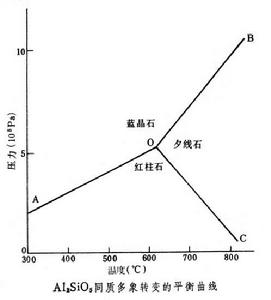
又考慮到一個礦物相併非都是一種組分所組成,因而C≥P,也就是在一定溫度和壓力範圍的封閉體系內,處於穩定平衡的礦物數等於或少於岩石的獨立組分數。例如,Al2SiO5的同質多象反應,如圖所示。當F=0時,即體系中所有強度因素都為一定值,P=1+2=3,稱為不變平衡體系,如圖中的O點;而 F=1時,體系中只有一個強度因素可以獨立變化,則P=1+1=2,稱為單變平衡,如圖中OA、OB及OC線;在F=2時,體系中的兩個強度因素都可以變化,稱為雙變平衡體系,如圖AOB、BOC、COA雙變區。
 礦物相律
礦物相律傅鷹著:《化學熱力學導論》,科學出版社,北京,1963。
賀同興等著:《變質岩岩石學》,地質出版社,北京,1980。
都城秋穗著,周雲生譯:《變質作用與變質帶》,地質出版社,北京,1979。(Akiho Miyashiro,Metamorphism and Metamorphic Belts, George Allen and Unwin Ltd.,London,1972.)