定律詳解
簡稱相律,或相平衡定律。它描述非均勻復相系(見相和相變）處於平衡時的性質：一個復相系在完全平衡時的自由度數F 等於其獨立組元數C 減去相數P 再加2。數學表達式為F =C-P＋2。 (1)
數字 2可認為是代表溫度和壓強兩個變數的數目。對於單元單相系,例如水，自由度數為2，故溫度和壓強可在合理的範圍內獨立地改變。對於單元二相系，例如水和水蒸氣的混合體,自由度數為1，表明溫度和壓強兩個變數中只有一個可以獨立地改變,故此時平衡態可在(T,p)相圖（見相和相變）上用一條曲線來表示。對於單元三相系,例如冰、水、水蒸氣的混合體,自由度數為0,表明溫度和壓強都有固定值而不能改變,此時平衡態在(T,p)相圖上就用一個點（通常稱為三相點）來表示。式(1)只適用於壓強均勻的情況。當固體受到扭力作用時，最多可能有六個脅強，故應將式(1)中的數字2改為7。如再考慮電場、磁場和重力場等因素，式(1)中的數字2還要相應地增大。此時，可將式(1)改寫為更加普遍的形式
F＋P =C＋n。 (2)
即復相系的自由度數與相數之和，等於其獨立組元數加上影響該系統平衡的外界因素的數目n。相律是由美國物理學家J.W.吉布斯在1875～1878年間發表的關於熱力學的論文中首先提出的。它是物理化學中最具普遍性的定律之一，適用於平衡態下的任何系統。它在討論復相平衡問題中起著一定的指導作用，在化工、冶金和其他工業方面都有廣泛的套用。
人物簡介
吉布斯(JosiahWillardGibbs)1839年2月11日生於美國康乃狄克州紐哈芬城.他在熱力學平衡與穩定性方面做了大量的研究工作並取得豐碩的成果,於1873-1878年間連續發表了3篇熱力學論文,奠定了熱力學理論體系的基礎.其中第三篇論文《論多相物質的平衡》是其最重要的成果.在這篇文章中,吉布斯提出了許多重要的熱力學概念,至今仍被廣泛使用.他完成了相律的推導.作為物理化學的重要基石之一,相律解決了化學反應系統平衡方面的眾多問題.他還提出了作為化學反應平衡判據的吉布斯自由能.吉布斯對於科學發展的另一大貢獻集中於統計力學方面,他於1902年出版了<<同熱力學合理基礎有特殊聯繫而發展起來的統計力學的基本原理>>一書.在書中,他提出了系綜理論,導出了相密度守恆原理,實現了統計物理學從分子運動論到統計力學的重大飛躍.他被譽為富蘭克林以後美國最偉大的科學家,是世界科學史上的重要人物之一。
套用領域
在物理化學，吉布斯相律說明了在特定相態下，系統的自由度跟其他變數的關係。吉布斯相律是相圖的基本原理，它指出:
F=C-P+n
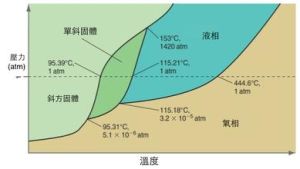套用和原理圖*F:自由度
*C:系統的組元數(例如化合物的數目)
*P:在該點的相態數目
*n:外界因素，多數取n=2，代表壓力和溫度;對於熔點極高的固體，蒸汽壓的影響非常小，可取n=1。
以水為例子，只有一種化合物，C=1。在三相點，P=3。F=1-3+2=0，所以溫度和壓力都固定。
當兩種態處於平衡，P=2，對應一個特定壓力，便恰好有一個熔點，即有一個自由度。吉布斯相律的預言正確:F=1-2+2=1。
吉布斯相律廣泛適用於多相平衡體系。
注:若兩相平衡時，壓強不相等，則，吉布斯相律不適用。如滲透平衡。
