定義
設A是n階方陣，如果數λ和n維非零列向量x使關係式 Ax=λx成立，那么這樣的數λ稱為矩陣A特徵值，非零向量x稱為A的對應於特徵值λ的特徵向量。式 Ax=λx也可寫成( A-λE)X=0。這是n個未知數n個方程的齊次線性方程組，它有非零解的充分必要條件是係數行列式| A-λE|=0。
矩陣特徵值設A是數域P上的一個n階矩陣，λ是一個未知量，
係數行列式|A-λE|稱為A的特徵多項式，記¦(λ)=|λE-A|，是一個P上的關於λ的n次多項式，E是單位矩陣。
¦(λ)=|λE-A|=λ+aλ+…+a= 0是一個n次代數方程，稱為A的特徵方程。特徵方程¦(λ)=|λE-A|=0的根(如：λ)稱為A的特徵根(或特徵值)。n次代數方程在複數域內有且僅有n個根，而在實數域內不一定有根，因此特徵根的多少和有無，不僅與A有關，與數域P也有關。
矩陣特徵值 矩陣特徵值以A的特徵值λ代入(λE-A)X=θ，得方程組(λE-A)X=θ，是一個齊次方程組，稱為A的關於λ的特徵方程組。因為|λE-A|=0，(λE-A)X=θ必存在非零解，稱為A的屬於λ的特徵向量。所有λ的特徵向量全體構成了λ的特徵向量空間。
性質
性質1：n階方陣A=(a)的所有特徵根為λ，λ，…,λ(包括重根)，則：
矩陣特徵值性質2：若λ是可逆陣A的一個特徵根，x為對應的特徵向量，則1/λ 是A的逆的一個特徵根，x仍為對應的特徵向量。
性質3：若 λ是方陣A的一個特徵根，x為對應的特徵向量，則λ 的m次方是A的m次方的一個特徵根，x仍為對應的特徵向量。
性質4：設λ，λ，…,λ是方陣A的互不相同的特徵值。x是屬於λ的特徵向量( i=1,2,…,m)，則x,x,…,x線性無關，即不相同特徵值的特徵向量線性無關 。
特徵值與特徵向量的求法
方法
對於矩陣A，由AX=λX，λEX=AX，得[λE-A]X=0即齊次線性方程組
矩陣特徵值有非零解的充分必要條件是：
矩陣特徵值即說明特徵根是特徵多項式|λE-A| =0的根，由代數基本定理
矩陣特徵值有n個復根λ,λ,…,λ，為A的n個特徵根。當特徵根λ(I=1,2,…,n)求出後，(λE-A)X=θ是齊次方程，λ均會使|λE-A|=0，(λE-A)X=θ必存在非零解，且有無窮個解向量，(λE-A)X=θ的基礎解系以及基礎解系的線性組合都是A的特徵向量。
示例
矩陣特徵值求矩陣的特徵值與特徵向量。
解：由特徵方程
矩陣特徵值解得A有2重特徵值λ=λ=-2，有單特徵值λ=4。
對於特徵值λ=λ=-2，解方程組(-2E-A)x=θ
矩陣特徵值得同解方程組x-x+x=0，解為x=x-x(x,x為自由未知量)。分別令自由未知量
矩陣特徵值得基礎解系
矩陣特徵值所以A的對應於特徵值λ=λ=-2的全部特徵向量為x=kξ+kξ(k,k不全為零)，可見，特徵值λ=-2的特徵向量空間是二維的。注意，特徵值在重根時，特徵向量空間的維數是特徵根的重數。
對於特徵值λ=4，方程組(4E-A)x=q
矩陣特徵值得同解方程組為
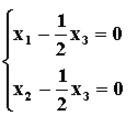矩陣特徵值通解為
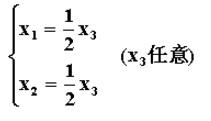矩陣特徵值
矩陣特徵值令自由未知量x=2得基礎解系ξ，所以A的對於特徵值λ=4得全部特徵向量為x= kξ
