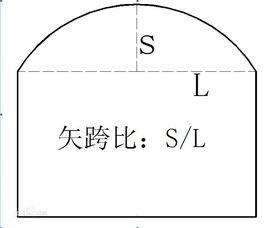
定義
淨矢高:從拱頂截面下緣至相鄰兩拱腳截面下緣最低點之連線的垂直距離。
計算矢高:從拱頂截面形心至相鄰兩拱腳截面形心之連線的垂直距離S。
淨跨徑:相鄰兩個橋墩(或橋台)之間的淨距。對於拱式橋是每孔拱跨兩個拱腳截面最低點之間的水平距離。計算跨徑:對於具有支座的橋樑,是指橋垮結構相鄰兩個支座中心之間的距離L:對於拱式橋,是指兩相鄰拱腳截面形心點之間的水平距離,即拱軸線兩端點之間的水平距離L。
 趙州橋
趙州橋矢跨比:計算矢高與計算跨徑之比(S/L),也稱拱矢度,它是反映拱橋受力特性的一個重要指標。
大矢跨比車行索道橋結構的可行性
要點
根據索道橋的通行標準,採用幾何非線性有限元方法,藉助 ANSYS 軟體分析大矢跨比車行索道橋靜力特性,對比並考察了其施工可行性與結構經濟性.結果表明大矢跨比索道橋的所有結構行為參數都達到常規索道橋的技術要求; 所有構件的安裝具有可施工性; 結構的經濟性優勢顯著,該結構可行性好.
車行索道橋屬於簡易柔性懸索橋的橋樑大類. 這種橋樑主索的矢跨比必須小於 1 /35,以滿足跨端行車的要求. 因此橋樑主索的恆載拉力占總設計拉力的比重往往很大,致使索材的利用效率較低.為了降低主索的拉力,加大橋樑主索的矢跨比,使之大於 1 /35; 同時,縮短橋跨兩端八字形橫樑的吊臂高度,憑藉穩定索把橋面索吊起,達到改善橋頭縱坡的目的.在此,把主索矢跨比大於 1 /35 的索道橋稱為大矢跨比索道橋。
成橋狀態恆載作用下的找形分析
採用 upgeom 命令將求得的節點位移值疊加到找形起始有限元模型的各節點上,更新模型後便得到成橋狀態恆載作用下橋樑平衡狀態的幾何形狀,此時,縱向橋面索為一條平順的曲線. 19#( 19‘’#) 橫樑至右( 左) 跨端區間的橋面索也由起始位形的折線變為平滑曲線; 在橫橋向,每道橋面板和橫樑的水平段的各相鄰節點的豎向相對變位小於1mm.找形分析得到的橋面索線形滿足索道橋橋面的行車要求.
由理想柔性索幾何線形的懸鏈線解析公式可知,在成橋狀態恆載基本不變的情況下,主索跨徑所對應的等代簡支梁跨中彎矩也不變,這時主索的水平索力決定其跨中矢高; 而不同的主索水平索力又對應於索單元不同的初應力值. 因此,不同橫樑位置所對應的等代簡支梁的跨中彎矩相近,同時在找形分析時索單元所設定的初應力值也相同,那么最終得到的索道橋成橋平衡態的跨中矢跨比也會很接近. 這為索結構找形分析時索單元初應變的合理選擇提供了判據.
結論
首先擬定了大矢跨比索道橋的結構方案,並分析了它的靜力特性.最後通過對比,考察了其施工可行性與經濟性.
( 1) 大矢跨比索道橋力學行為的空間效應更加顯著. 用於傳統索道橋結構分析的平面解析法不宜用於這種結構的內力分析.只有採用能考慮到結構構件空間效應的幾何非線性有限元法對其做精細分析,才能正確把握其力學特性.
( 2) 縮短索道橋跨端附近橫樑的吊臂長度能改善橋頭縱坡,但改善幅度有限.因受跨端橋面縱坡的限制,索道橋的主索跨中矢跨比很難達到常規公路懸索橋的主索矢跨比.
( 3) 大矢跨比索道橋的結構行為參數達到常規索道橋的技術要求; 其所有構件的安裝完全可採用現有的常規施工技術來實現,具有可施工性; 並且該結構的經濟性優勢顯著.由此可知該結構形式是完全可行的.
拱輔梁橋拱肋合理矢跨比的確定
拱肋矢跨比對拱輔梁橋的力學特性影響大,為尋求其合理範圍,以梁拱相同剛度比而不同矢跨比為條件,從自振模態和多遇及罕遇地震作用下結構動力回響角度,結合工程實例,運用時程分析法及多自由度體系簡化的滯回曲線,矢跨比變化對全橋變位及內力影響的規律,並提出相應的合理設計範圍. 拱肋矢跨比主要影響橫橋向、豎向位移及內力,且矢跨比為 1 /5 時橋樑抗震性能最優; 對於多自由度體系變位組合中的主要成分得出的簡化滯回曲線,由其定性分析得出的結論能與一般時程分析得出的結論一致.
問題的提出
拱輔梁橋為由梁、拱肋及吊桿組成的以梁受力為主、拱受力為輔的梁橋體系,在結構形式上屬於梁、拱組合體系. 從主拱圈材料角度依鋼管混凝土拱橋規範判斷為鋼管混凝土結構( CFSTS) ; 從結構受力貢獻大小判斷為以鋼筋混凝土梁受力為主、拱肋受力為輔的梁橋.
下承式拱輔梁橋,按基本結構形式可分為: ①拱輔簡支梁橋; ② 拱輔連續梁橋; ③ 拱輔剛架橋;④ 其他組合形式的拱輔梁橋,如由索塔、斜拉索、吊桿、拱肋與主梁的組合形似,故此種結構體系屬於外部超靜定、內部超靜定結構。
作為梁拱組合體系的分支,拱輔梁橋越來越在公路與鐵路上的套用也逐漸增多, 列舉了其中具有代表性的實例. 關於拱肋矢跨比的最優取值範圍,更多偏重於從靜力特性、施工及經濟性要求去分析,而從動力特性面研究的資料尚少.以拱輔梁橋為例,從動、力特性角度探討不同矢跨比的最優值.
對於一座拱輔梁橋,拱肋矢跨比最合理值究竟如何,可能很難清楚地選擇,特別是鐵路拱輔梁橋. 因為與公路橋樑設計規範相比,鐵路橋樑設計規範對鐵路橋樑還有橫橋向剛度的要求,在規範及國內外相關資料的取值範圍內,選取 5 種不同矢跨比 1 /3、1 /4、1 /5、1 /6 及1 /7,進一步研究結構三向力學特性的變化規律。
拱輔梁橋的地震回響
拱輔梁橋在三向地震作用下,梁、拱單元可簡化為兩彈簧質點. 一般先按單向水平地震作用計算出各自方向的地震回響,然後將三向上各自地震回響組合成空間地震回響,其中多自由度體系( MDOF) 地震反應的基本理論計算按振型分解法求解,其基本思想是將多自由度體系的地震振型轉化為單自由度體系地震反應問題。
1) 通過拱肋變位推導公式可知,影響拱肋變位的因素包括拱肋截面所受彎矩剪力和矢跨比.
2) 通過自振頻率分析發現拱肋橫向力學性能決定組合結構動力性能,且矢跨比越小橋樑整體剛度越好,通過地震作用下位移及內力分析發現矢跨比越小其位移及內力越大.
3) 拱肋矢跨比主要影響橫橋向、豎向位移及內力,合理的矢跨比可使得橫橋向和豎向梁拱的力學性能達到最優. 綜合考慮,矢跨比為 1 /5 時橋樑抗震性能最優, “矢跨比取到 1 /5 左右時較為恰當的,這也是實際拱橋設計中常採用的矢跨比取值”.從結構極限承載力、穩定性或用鋼量及動力特性角度研究不同結構的合理矢跨比,不難發現,雖然結構形式不同,但結構的合理矢跨比卻展現出比較穩定的範圍,認為矢跨比在 f /l = 1 /5 左右附近合理.
4) 簡化滯回曲線也可用於結構動力研究方案之間的最佳化設計,這種處理方法可大大提高尋求最佳化方案的有效性.
矢跨比對懸索橋結構剛度的影響
主纜的矢跨比是設計懸索橋時需要首先確定的一個重要設計參數,其對結構剛度有較大影響。對大跨懸索橋的結構剛度隨矢跨比的減小而增大的普遍認識存在一定的片面性,提出懸索橋的結構剛度應綜合考慮重力剛度及幾何剛度的貢獻,兩種剛度效應的疊加才能較真實地反映結構剛度。懸索橋建立有限元計算模型,計算矢跨比取 1 /15 ~ 1 /5 時,懸索橋加勁梁的豎向撓度、梁端的縱向位移及梁端的豎向轉角,以重力剛度及幾何剛度各自隨矢跨比的變化規律及其在結構剛度中所占的比重,從而得出結構剛度隨矢跨比的真實變化規律,並給予合理解釋,得出一些有用的結論,為結構的最佳化設計提供參考。
現有的重力剛度理論的基礎上,將橋塔的縱向位移對線形的影響考慮進來,得出活載下塔頂縱向位移引起的主纜豎向撓度與主纜矢跨比的二次方成反比。從而從理論上說明結構剛度隨矢跨比出現非單調變化規律的可性。實際上,隨著矢跨比的改變,除了重力剛度會隨之改變以外,結構的幾何線形也出現了變化,即體系本身所蘊含的勢能不同,其在結構抵抗變形時產生的貢獻有差異,將幾何形狀提供的剛度稱為幾何剛度。提出分析矢跨比對懸索橋結構剛度的影回響綜合考慮重力剛度及幾何剛度各自的貢獻,並通過對某懸索橋的有限元分析研究結構剛度、重力剛度及幾何剛度隨矢跨比的變化規律,從而給出工程中懸索橋合理矢跨比範圍。
矢跨比對重力剛度的影響
重力剛度的概念
對於大跨徑懸索橋,加勁梁的豎向抗彎剛度將隨著跨度的增加而在懸索橋整體剛度中降到次要位置。在靜力分析中,可以先令加勁梁的抗彎剛度為零,取主纜作為基本體系。柔性的主纜因承受巨大的恆載而產生的抵抗活載變形的剛度,稱為重力剛度。
從懸掛纜索來看,在均布恆載 q 下的線形是拋物線,即曲線①; 其後,作用集中活載 P( qL > P)形成曲線③; 相較於無恆載懸索上僅作用 P 時的曲線②、曲線③的變形要小得多,即懸索在恆載下獲得了保證穩定線形的重力剛度。
矢跨比對幾何剛度的影響
幾何剛度的概念
所謂幾何剛度是指大跨徑懸索橋在自身恆載作用下達到設計矢跨比 f /L 時,將柔性主纜及吊索均簡化成相應的鉸接鏈桿,加勁梁簡化為連續梁,此組合體系抵抗豎向活載變形的剛度,對於大跨懸索橋而言,加勁梁的豎向抗彎剛度較小,忽略加勁梁的剛度,並將主纜簡化為最簡單的靜定結構,即兩根鏈桿,在均布恆載下的主纜線形為拋物線,即曲線①; 在矢高 f 處加入一個單鉸,將索曲線①簡化為兩根鏈桿,即折線②; 其後,作用集中活載 P,體系②變形至③線,C點移動到C‘’ 點,距離CC‘’ 即為與索的幾何剛度相關的豎向位移,此位移與矢跨比 f /L 有密切的關係。