基本介紹
定義1 設R是集合A上的一個二元關係,如果R是自反的、對稱的,則稱R 是 相容關係 。
容易看到,等價關係是一種特殊的相容關係,即具有傳遞性的相容關係。在人際關係中,朋友關係是相容關係,但它不是等價關係,因為它滿足自反性、對稱性但不滿足傳遞性。
又如,設A是由一些英文單詞為元素組成的集合,A={dog,cat,deer,rat,coat,door}, R是A上的二元關係,其定義為:當兩個單詞具有相同的字母,則認為它們是相關的。
 相容關係
相容關係顯然,R是自反的、對稱的,所以R是相容關係。但R不是等價關係, 因為它不是可傳遞的,如<dog, coat>∈R, <coat,rat>∈R,但<dog,rat> R。
在相容關係的關係圖上,每個結點處都有自迴路且每兩個相關結點間的弧線都是成對出現的。為了簡化圖形,我們對 相容關係圖,不畫自迴路,並且用單線代替成對的弧線。
定義2 設R是集合A上的一個相容關係,C是A的子集,如果對於C中任意兩個元素x,y,有<x,y>∈R,稱C是相容關係R產生的 相容類。
例如上例的相容關係R,可產生相容類{dog,deer}, {cat, rat, coat}, {door}等 。
對於相容類{dog,deer}, 能加進新的元素組成新的相容類,而相容類{cat,rat,coat}加入任意一個新元素,就不能組成相容類,這裡稱作最大相容類。
定義3 設R是集合A上的一個相容關係,不能真包含在任何其他相容類中的相容類,稱作 最大相容類,記作C。
又如,設A={134,345,275,347, 348,129}, R是A上的二元關係,其定義為: a, b∈A, 且a和b至少有一一個數字相同,則a和b相關。顯然R是相容的。A的子集: {134, 347, 348}, {275, 345}, {134, 129}等都是相容類。
對於前兩個相容類,都能添加新的元素組成新的相容類。如在相容類{134,347,348}中添加元素: 345, 可組成新的相容類: {134, 345, 347, 348};在相容類(275,345}中添加新的元素: 347,可組成新的相容類: {275, 345,347}。因此相容類{134,347, 348}, {275,345}不是最大相容類。
而對於相容類{129,134}, 添加任意的元素就不再組成相容類,因此相容類{129,134} 是最大相容類。
對於最大相容類也可以認為: R是A上的相容關係,B是相容類,在差集A-B中沒有元素能和B中所有元素都相關的,則稱B為 最大相容類。
在相容關係圖中,完全多邊形的結點集合,就是相容類。完全多邊形是指每個結點與其他結點聯接的多邊形。例如一個三角形是完全多邊形,一個四邊形加上兩條對角線就是完全多邊形。最大完全多邊形的結點集合,就是最大相容類。
此外,在相容關係圖中,一個孤立結點,以及不是完全多邊形的兩個結點的連線,也是最大相容類 。
例題解析
例1 設給定相容關係圖如圖1所示,寫出最大相容類。
 圖1
圖1解 最大相容類為: {1, 2,6},{1, 4, 5,6}, {1, 7}, {3,6},{8} 。
相關定理
定理 設R是有限集A上的相容關係,C是一個相容類,那么一定存在一個最大相容類C,使得C⊆C。
證明
設A={a₁,a₂, .. a},構造相容類序列
 相容關係
相容關係 相容關係
相容關係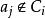 相容關係
相容關係其中C=C ,且 ,其中j是滿足 而a與C中各元素都有相容關係,且j是滿足上述條件的最小下標。
由於A的元素個數|A|=n,所以至多經過n-|C|步,就使這個過程結束,而這個序列的最後一個相容類,就是所要找的最大相容類 。

