基本概念
平面上的變換如果對應線段A’B’與AB的比是個正的常數:
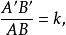 相似性質
相似性質則這種變換叫做 相似變換,常數k叫做相似比。
 相似性質
相似性質 相似性質
相似性質 相似性質
相似性質 相似性質
相似性質在相似變換下,如果圖形 變為圖形 ,則說圖形 相似於圖形 。
從相似變換的定義可以直接看出,移動不過是相似變換當相似比k等於1的特殊情形。顯然位似變換是相似變換的特例。
相似性質介紹
相似變換具有下面的性質:
 相似性質
相似性質 相似性質
相似性質(1)相似變換 的逆變換 仍是相似變換 。
 相似性質
相似性質事實上,設相似變換 的對應線段為AB和A’B’,相似比為k:
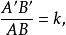 相似性質
相似性質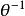 相似性質
相似性質則逆變換 的對應線段為A'B’和AB,並且它是以k的倒數
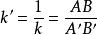 相似性質
相似性質為相似比的相似變換。
 相似性質
相似性質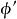 相似性質
相似性質 相似性質
相似性質 相似性質
相似性質根據這個性質可知,如果圖形 相似於 ,則 也相似於 。
 相似性質
相似性質 相似性質
相似性質(2) 兩個相似變換 和 的積仍是一個相似變換。
 相似性質
相似性質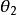 相似性質
相似性質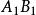 相似性質
相似性質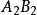 相似性質
相似性質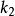 相似性質
相似性質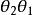 相似性質
相似性質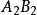 相似性質
相似性質事實上,設相似變換 把線段AB變為AB,相似比為k;相似變換 把線段 變為 ,相似比為 。這時兩個相似變換的積 把線段AB變為 ,而且
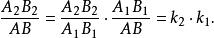 相似性質
相似性質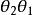 相似性質
相似性質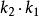 相似性質
相似性質因此, 是以 為相似比的相似變換。所以,平面上所有相似變換構成一個群叫做 相似變換群。
 相似性質
相似性質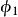 相似性質
相似性質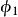 相似性質
相似性質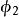 相似性質
相似性質 相似性質
相似性質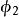 相似性質
相似性質根據這個性質可知,如果圖形 相似於 , 相似於 ,則 相似於 。
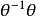 相似性質
相似性質 相似性質
相似性質 相似性質
相似性質其次,由上面兩個性質可知,相似變換 是恆等變換,恆等變換把每個圖形 變為本身,因此,每個圖形 相似於本身 。
(3) 在相似變換下,一條直線上的點,仍變到一條直線上,也就是直線變為直線。
事實上,設A、B、C是一條直線a上的三個點,並且點B在A與C之間,A’、B‘,C’是它們的對應點(圖1)根據相似變換的定義:
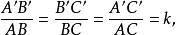 相似性質
相似性質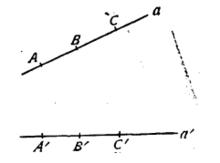 圖1
圖1這裡k是相似比,由此得到,
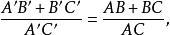 相似性質
相似性質因為,AB+BC=AC,
所以A'B'+B'C'=A'C',
因此,點A‘、B’、C’也在一條直線上,並且點B’在A‘與C’之間。
根據這個性質可知,在相似變換下,半直線變為半直線,角變為角,任意三角形變為與其相似的三角形。
(4)在相似變換下,一條直線上的三個點A、B、C的簡單比不變 。
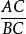 相似性質
相似性質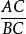 相似性質
相似性質定義 一條直線上三個點A、B、C的簡單比是,這個簡單比常用記號(ABC)表示,A、B叫做基礎點,C叫做分點,簡單比與線段的分比略有不同,AB由分點C所得到的分比是,從有向線段來看,兩者差一個符號。C內分AB時簡單比是負值,外分時是正值。
設三點A、B、C在相似變換下,變為點A’、B‘、C‘,根據相似變換定義,
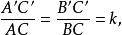 相似性質
相似性質由此得到
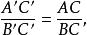 相似性質
相似性質也就是
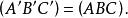 相似性質
相似性質(5) 在相似變換下,角的大小不變。
事實上,在相似變換下,任意三角形ABC變為相似三角形A‘B’C‘,且
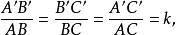 相似性質
相似性質因此三角形的角不變。
(6) 在相似變換下,對應三角形的面積比不變。
事實上,設三角形ABC變為A’B’C’,用h和h'表示這兩個三角形的高(圖2)根據上述性質,在相似變換下,h變為h',因此,
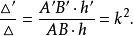 相似性質
相似性質 相似性質
相似性質這裡,表示對應三角形的面積,由這個等式可知,三角形面積的比是相似變換的不變數。
我們看出,相似變換的不變性質和不變數是相似幾何里的主要研究對象。
研究決定相似變換的條件,我們有:
定理 相似變換由不共線的三對對應點唯一確定 。

