相關知識
相似
根據物理現象相似的定義,兩個流場相似等價於兩個流場對應點在對應時刻所有表征流動狀態的相應物理量各自保持固定比例。一般要求幾何相似、運動相似、動力相似、熱力學相似以及質量相似,兩個流動才相似。
相似定理
判斷兩個現象相似的依據是相似定理。相似定理連線的是現象的相似與單值條件的相似和相似準則的相同之間的對應關係。
相似第一定理:兩個相似的系統,單值條件相同,其相似判據的數值也相同。
相似第二定理:當一現象由n個物理量的函式關係來表示,且這些物理量中含有m種基本量綱時,則能得到(n-m)個相似判據。
相似第三定理:凡具有同一特性的現象,當單值條件(系統的幾何性質、介質的物理性質、起始條件和邊界條件等)彼此相似,且由單值條件的物理量所組成的相似判據在數值上相等時,則這些現象必定相似。
定義
如果兩個現象相似,則這兩者的無量綱形式的方程組和單值條件應該相同,具有相同的無量綱形式解。出現在這兩者的無量綱形式的方程組及單值條件中的所有無量綱組合數對應相等。這些無量綱組合數成為相似準則。如在實驗流體力學中的雷諾數Re、馬赫數Ma等。
簡介
理論上,任意一個流動由控制該流動的基本微分方程和相應的定解條件唯一確定。兩個相似的流動現象,為了保證它們遵循相同的客觀規律,其微分方程就應該相同,這是同類流動的通解;此外,要求得某一具體流動的特解,還要求其單值條件也必須相似。這些單值性條件包括:
(1)初始條件,指非定常流動問題中開始時刻的流速、壓力等物理量的分布;對於定常流動不需要這一條件。
(2)邊界條件,指所研究系統的邊界上(如進口、出口及壁面處等)的流速、壓力等物理量的分布。
(3)幾何條件,指系統表面的幾何形狀、位置及表面粗糙度等。
(4)物理條件,指系統內流體的種類及物性,如密度、粘性等。
因此,如果兩個流動相似,則作為單值性條件相似,作用在這兩個系統上的慣性力與其它各力的比例應對應相等。在流體力學問題中,若存在上述所有這六種力,而且滿足動力相似,則必須使下列各力間的比例對應相等。
慣性力與壓力(或壓差)之比: Fi/Fp
慣性力與重力之比: Fi/fg
慣性力與摩擦力之比: Fi/Fv
慣性力與彈性力之比:Fi/Fe
慣性力與表面張力之比:Fi/Ft
上述五式式分別引入了五個無量綱數,它們依次是:
1)歐拉數Eu=2Δp/(ρ·V^2),例如以後經常用到的表示物體表面壓力分布的壓強係數,以及升力係數和阻力係數等。物理上,歐拉數表征了慣性力與壓強梯度間的量級之比。
2)弗勞德數Fr=V/sqrt (l·g),物理上,弗勞德數表征了慣性力與重力間的量級之比,是一個表征流速高低的無量綱量。
3)雷諾數Re=Vl/υ,物理上,雷諾數表征了相似流動中慣性力與粘性力間的量級之比,流動的Re數小,表示與慣性力的量級相比,粘性摩擦力的量級要大得多,因此可以忽略慣性力的作用;反之,Re數大則表示慣性力起主要作用,因此可以當作無粘流體處理。
4)馬赫數Ma=V/c,物理上,馬赫數表征了慣性力與彈性力間的量級之比,是氣體可壓縮性的度量,通常用來表示飛行器的飛行速度或者氣流的流動速度。
5)韋伯數We, 物理上,韋伯數表征了慣性力與表面張力間的量級之比。
可以看出,Eu、Fr、Re、Ma和We都是無量綱數,在相似理論中稱作相似準則或者相似判據,它們是判斷兩個現象是否相似的依據。因而,彼此相似的現象,其同名相似準則的數值一定相等。反之,如果兩個流動的單值條件相似,而且由單值條件組成的同名相似準則的數值相等,則這兩個現象一定相似。
推導方法
推導相似準則目前通常有兩種方法,利用已有的數學方程來推導相似準則的方程分析法;對過程包含的所有變數進行量綱和諧的量綱分析法。
方程分析方法
對於某一現象,若已經存在明確的數學模型,則一般採用方程分析法來推導相似準則。方程分析包括相似轉化法和積分類比法兩大方法。其中積分類比推導過程簡單,且推導出的相似準則通常有較為明確的物理意義,因此被廣為採用。
積分類比方法的步驟:
首先寫出某類現象或過程的全部控制方程及單值條件,然後用方程式中的任一項除以其他各項,對於同類型的情況,只需取其中一項即可,最後用積分類比來代替每兩項的比值。在處理過程中,對沿各軸向的分量,用量本身代替,坐標用定性尺寸代替。
量綱分析法
量綱分析法就是將現象所涉及的全部物理量,通過因次和諧的方法整理成一個完整的無因次群,也就是相似準則數群,而數群的個數則可由白金漢定理給出。
量綱分析法的步驟為:
列出現象所涉及的全部的物理量及其因次,並確定基本量綱及其參數群,然後將自乘未知整數冪次的基本參數群同其他的各變數相乘,相乘後的量為無因次量的方法來推導相似準則。即為各物理量因次的冪的和為零。
相似準則的檢驗
李之光在《相似與模化(理論及套用)》一書中提到,對於應該忽略哪些相似準則、保留下來的相似準又該採用什麼樣的形式,模化的結果是否能夠推廣到原型中去,需要給出一定的證明。
利用實驗的方法來證明的方法包括兩個:
1、局部旁證法
局部旁證法就是利用建立的模型進行單項實驗,僅僅改變其中的一個參數,而其他參數不變,觀察該參數對實驗結果的影響程度,影響程度大的應當給予考慮,反之,應適當的忽略
李之光以旋風分離器為例,通過單項實驗研究了包含粒徑的Stk(斯托克斯)準則、包含流速的傅魯德準則和雷諾準則等準則對實驗結果的影響程度,結果表明Stk準則是必須保證的定性準則,而其他準則均可不予考慮。
2 、總體旁證法
總體旁證法就是先建造一個大的模型,然後再按照一定的比例建造一個小的模型。首先利用大的模型進行一系列的實驗。同時在小的模型上,遵照經過分析確定的近似模化條件來進行實驗。所得到的實驗結果如果和大模型的結果相似,那么就證明已經確定的模化條件是可行的,也就是說所選取的相似準則是正確的。
Kimber在推導了添加化學劑的蒸汽驅相似準則後,先建立了一個大的三維比例模型,然後在此基礎上又按照比例縮小建立了小的三維比例模型。在以大模型的實驗結果為基礎的情況下,通過對比大小模型的驅替狀況,來考察選擇不同的主要相似準則方法的差別,確定了不同的相似準則在模擬不同現象或過程的優缺點。
3、數值模擬的方法
李宜強等人通過定義畸變係數,也就是模型、原型中相對應的相似準則的比值來考察相似準則的影響程度。選取不同大小的畸變係數,然後先後對各個相似準則進行畸變,在此過程中只對一個相似準則畸變,而其他的不變,這樣計算畸變前後採收率曲線圍成的面積的變化程度,以此來作為該相似準則的影響係數,影響係數越大,在模化的時候就應該優先考慮。但是這種方法很難做到只改變一個相似準則而保持其他相似準則不變,因此這種方法實質不是相似準則的影響係數,而是某一個量的影響程度。
白玉湖等人採用數值實驗的方法,先對方程進行無因次化,轉化成係數為各相似準則的無量綱的方程組,然後進行差分求解。通過對各個相似參數做出微小的改變來觀察其對採收率或采出程度等目標函式的影響,通過比較影響程度的大小來衡量和判斷該相似參數的的重要程度,也就是該相似準則的敏感性大小。敏感程度大的為主要的相似準則,在進行參數轉換時,應著重考慮。
郭文敏、秦積瞬等人通過定義畸變前後的采出程度的變化幅度為影響係數的方法考察了聚合物驅的相似準則敏感性分析,並利用乘積關係得出了聚合物驅采出程度的數學模型,可以方便的預測不同情況下的采出程度。
風洞試驗相似準則
風洞試驗的理論基礎是相似原理,而相似理論的基礎是量的線性變換或稱相似變換。兩個物理現象相似是指在對應點上對應瞬時所有表征現象的相應物理量都保持各自固定的比例關係(如果是向量還包括方向相同)。相似的正定理指出相似的現象,其同名相似準則數值相同,這是相似現象的必要條件。而根據相似的逆定理,兩個物理現象相似的充分條件是兩個現象的單值條件相似,而且由單值條件組成的同名相似準則的數值相同。所謂單值條件是指把滿足同一物理方程的各種現象單一地區分開來所必須具有的基本條件,它包括幾何條件、物理條件、邊界條件和時間條件。相似準則一般可由描述現象特徵的各個量之間關係的物理方程推導出或由量綱分析推導出。
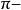 相似準則
相似準則根據定理,對於各種飛行器模型的風洞試驗,相似準則是一個必須遵守的普遍原理。兩個流場相似可以用五個方面的相似來描述:一是幾何相似,即試驗模型與真實飛行器之間對應尺寸成比例,對應線段的方位相同;二是運動相似,即兩個流場各對應點的速度彼此成比例,而對應速度矢量的方位角相等;三是動力相似,即兩個流場各對應點所作用的各種力的大小之比為常值,且方位角彼此相等;四是熱力學相似,即兩個流場對應點上的溫度之比為常值;五是質量相似,即兩個流場或物體對應點密度之比為常值。
按相似定理的要求,兩個現象“完全相似”的條件是單值條件相似以及所有的相似參數完全相同。模型試驗做到與實物完全相似稱之為完全模擬。一般情況下這是很難做到的,有時根本無法做到,通常只能做到使其主要的相似參數相同,而忽略次要的相似參數,或對其進行修正,例如,風洞縮比模型試驗通常就不可能同時模擬Re數和F:數。對於流場中某個區域來說,往往也只是一個或幾個相似參數起主要作用,例如,在粘性影響起主要作用時應考慮Re數,壓縮性影響較顯著時應考慮Ma數等,這稱之為局部模擬或叫近似模擬。