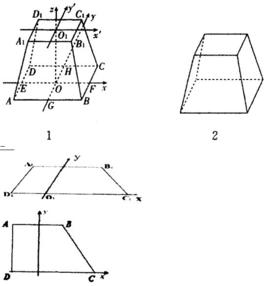
簡介
眾所周知,夸美紐斯(Comenius)和裴斯塔洛奇(Pestalozzi)都是直觀主義的倡導者。在我國的現代漢語詞典中,對直觀的解釋是“用感官直接接受,直接觀察”。在日本的廣辭苑中,對直觀的解釋是“一般地不含有判斷、推理的思維作用,直接把握對象的作用”。在日本的哲學詞典中對直觀的解釋是“直觀是直接地把握對象的全貌和本質的認識作用”。在數學教育文獻中,認為直觀是直接“從感覺的具體的對象背後,發現抽象的,理想的(狀態)的能力”。數學家克萊因認為: “數學的直觀,就是對概念、證明的直接把握”。直觀在英語中是“ directly perceived through the senses; audio-visual”,也有直接的含義。
從以上幾種對直觀的解釋中,儘管從事語言學、哲學、教育學、數學教育學、數學的人,對直觀有不同的理解,但是,“直接”對研究對象的“把握”是共同的。由於研究對象的不同,這種“直接的把握”的水平有所不同而已。正如裴斯塔洛奇指出的那樣:“直觀是全部認識的基礎”,“知識是主體自發活動的產物”,教育中“培養人的直觀的基礎,比什麼都重要”。但是,在教學論的著作中,無一例外地會提及“直觀性原則”,在王策三著的《教學論稿》中,認為直觀性原則“這是為處理好教學中詞、概念和事物及其形象之間的矛盾關係而提出的”。這種提法對數學教學並不完全合適。
意義
一般地,認為數學是一門邏輯嚴謹的演繹學科。尤其是以歐幾里德的《幾何原本》為典範。但是《幾何原本》是在古埃及、古巴比倫時期的“直觀幾何”的基礎上發展起來的。數學的其它分支的形成、發展也應當如此。數學發展的歷史進程,反映了人類對數學的認識過程——直觀和邏輯之間相輔相成。事實上,存在於“直觀幾何”與“歐氏幾何”之間的“希臘初期階段的幾何”,已經出現了演繹證明的邏輯成分。數學發展的歷史過程,可以反映出人類對數學的認識過程。
新課標(2011)中的定義
幾何直觀主要是指利用圖形描述和分析問題。藉助幾何直觀可以把複雜的數學問題變得簡明、形象,有助於探索解決問題的思路,預測結果。幾何直觀可以幫助學生直觀地理解數學,在整個數學學習過程中都發揮著重要作用。