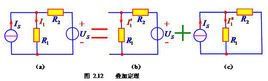
簡介
電路的 疊加定理(Superposition theorem)指出:對於一個線性系統,一個含多個獨立源的雙邊線性電路的任何支路的回響(電壓或電流),等於每個獨立源單獨作用時的回響的代數和,此時所有其他獨立源被替換成他們各自的阻抗。
為了確定每個獨立源的作用,所有的其他電源的必須“關閉”(置零):
在所有其他獨立電壓源處用短路代替(從而消除電勢差,即令V = 0;理想電壓源的內部阻抗為零(短路))。
在所有其他獨立電流源處用開路代替 (從而消除電流,即令I = 0;理想的電流源的內部阻抗為無窮大(開路))。
1.在所有其他獨立電壓源處用短路代替(從而消除電勢差,即令V = 0;理想電壓源的內部阻抗為零(短路))。
2.在所有其他獨立電流源處用開路代替 (從而消除電流,即令I = 0;理想的電流源的內部阻抗為無窮大(開路))。
依次對每個電源進行以上步驟,然後將所得的回響相加以確定電路的真實操作。所得到的電路操作是不同電壓源和電流源的疊加。
疊加定理在電路分析中非常重要。它可以用來將任何電路轉換為諾頓等效電路或戴維南等效電路。
該定理適用於由獨立源、受控源、無源器件(電阻器、電感、電容)和變壓器組成的線性網路(時變或靜態)。
應該注意的另一點是,疊加僅適用於電壓和電流,而不適用於電功率。換句話說,其他每個電源單獨作用的功率之和並不是真正消耗的功率。要計算電功率,我們應該先用疊加定理得到各線性元件的電壓和電流,然後計算出倍增的電壓和電流的總和。
戴維南定理
戴維南定理(Thevenin's theorem)又稱 等效電壓源定律,是由法國科學家L·C·戴維南於1883年提出的一個電學定理。由於早在1853年,亥姆霍茲也提出過本定理,所以又稱 亥姆霍茲-戴維南定理。其內容是:一個含有獨立電壓源、獨立電流源及電阻的線性網路的兩端,就其外部型態而言,在電學上可以用一個獨立電壓源 V和一個鬆弛二端網路的串聯電阻組合來等效。在單頻交流系統中,此定理不僅適用於電阻,也適用於廣義的阻抗。
此定理陳述出一個具有電壓源及電阻的電路可以被轉換成戴維南等效電路,這是用於電路分析的簡化技巧。戴維南等效電路對於電源供應器及電池(裡面包含一個代表內阻抗的電阻及一個代表電動勢的電壓源)來說是一個很好的等效模型,此電路包含了一個理想的電壓源串聯一個理想的電阻。
諾頓定理
諾頓定理(Norton's theorem)指的是一個由電壓源及電阻所組成的具有兩個端點的電路系統,都可以在電路上等效於由一個理想電流源 I與一個電阻 R並聯的電路。對於單頻的交流系統,此定理不只適用於電阻,亦可適用於廣義的阻抗。 諾頓等效電路是用來描述線性電源與阻抗在某個頻率下的等效電路,此等效電路是由一個理想電流源與一個理想阻抗並聯所組成的。
諾頓定理是戴維寧定理的一個延伸,於1926年由兩人分別提出,他們分別是西門子公司研究員漢斯·梅耶爾(1895年-1980年)及貝爾實驗室工程師愛德華·勞笠·諾頓(1898-1983)。實際上梅耶爾是兩人中唯一有在這課題上發表過論文的人,但諾頓只在貝爾實驗室內部用的一份技術報告上提及過他的發現。