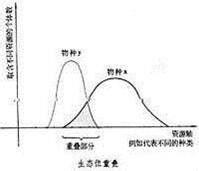
生態位重疊的基本內涵
生態位重疊是生態位計測過程中的一個重要指標。許多學者曾經對此給出不同定義,如:2個物種對某一資源的共同利用程度(Cowelletal.,1971;Abrams,1980);2個物種在同一資源狀態上的相遇頻率(Hurlbert,1978);一定資源狀態上物種的多樣性程度(Pielou,1971);2個物種與其生態因子聯繫上的相似性(王剛,1984)。為了使生態位重疊能夠涵蓋實際生態位和基礎生態位2種情況,研究者將生態位重疊定義為2個或多個物種或種群在適應環境和利用資源的實際幅度或潛在能力方面所表現出的共同性或相似性。
資源分享的數量或生態位重疊是理論生態學研究的中心問題之一。生態學家們長期以來一直困擾於2個種的生態學特徵究竟可以相似到多大程度而仍然可以共同生存?競爭排斥法則、特徵替位、極限相似性、種填塞以及最大容許生態位重疊等概念都是在這一問題的啟發下構建起來的。一些數學模型的運算結果表明:當競爭種類數量增加時,最大容許生態位重疊應當降低,並接近於衰減指數。最大容許生態位重疊應該對環境的變化不敏感。
生態位重疊與競爭
當兩個物種利用同一資源或共同占有某一資源因素(食物、營養成分、空間等)時,就會出現生態位重疊現象(niche overlap)。在這種情況下,就會有一部分空間為兩個生態位所共占,假如兩個物種具有完全一樣的生態位,就叫完全重疊(complet overlap)。但多數情況下,生態位之間只會發生部分重疊,即一部分資源是被共同利用的,而其他部分則是被各自所占據。在由兩個生態位維度(兩個資源軸)組成的三維生態空間,雖然每一個分離的生態位維度之上的三維峰的陰影重疊著,但在兩個維度中的實際重疊很小。
Hutchinson (1957)認為生態位重疊是兩個種間發生競爭的前提條件。他假設環境已充分飽和,即任何一段時間的生態位重疊都不能忍受。因此,在任何兩個生態位重疊部分都必然要發生競爭排斥作用(competitive exclusion)。這種生態位重疊引起的競爭常被稱做資源利用性競爭(exploitation competition)。但實際上生態位重疊並不一定能導致競爭,除非共用資源供應不足。沿著一個維度生態位顯著或完全重疊的一對種,能夠通過沿另一維度的生態位分割而避免競爭。不過,在研究種間競爭時,生態位重疊常被作為一個重要的因子加以分析。
生態位重疊指數
(1)Levins(1968)重疊指數
(2) Schoener(1974)重疊指數
(3)Hurlbert(1978)重疊指數
該指數要考慮每一個資源狀態的量值的相對大小,Hurlbert把其叫做資源的相對多度。這是為了改進Levins指數而提出來的。Hurlbert(1982) 指出, 兩個種按相同比例利用每一資源狀態時,重疊指數最大,其值等於1。
(4)Petraitis(1979)特定重疊指數
該指數對野外數據的適合程度較低,在實驗研究中,效果較好,該指數也介於0和1之間。
(5)Pianka(1973)重疊指數
Pianka指數的值也介於0和1之間。
(6)百分比重疊指數
百分比重疊(Percentage overlap)是最簡單的生態位重疊計測方法,並便於解釋,因為它實際上測定的是兩個種資源利用曲線重疊的面積。這一指數經Schoener(1970)使用,並命名為Schoener指數,但實際上其源於1938年Renkonen的工作,還有人稱其為Renkonen指數。
(7)Morisite(1959)重疊指數
這一指數一般只用於密度或多度數據,即用個體數為指標,如果數據是其它類型,可以選用下面簡化的Morisita指數。
(8)簡化的Morisita指數
這一指數是Horn(1966)年提出的,故也稱為Morisita-Horn指數。這一指數與Levins和Pianka指數較為接近。經過比較研究,Linton等人認為這一指數比Pianka指數精度高,他們推薦使用該指數。
(9)Horn(1966)重疊指數
該指數也是基於信息理論之上的,對數可以用常用對數、自然對數或其它對數。
(10) 王氏重疊指數
王剛(1984)把生態位重疊理解為兩個種在其生態因子聯繫上的相似性。
(11)生態位分離測度(余世孝和Orloci 1989,1993)
生態位分離(Niche Separation),是測定物種生態位的非相似性,所以,它也反映了生態位的重疊。
(12) 多種群生態位重疊指數
以上的指數均是針對兩個種而言,即測定兩個種的生態位重疊。生態位重疊指數還有許多種,以上是較為常用的。在生態位重疊指數選擇上,應遵守一個原則,即計測的結果要利於物種生物學、生態學及資源利用等方面的解釋。Hurlbert (1978)認為當重疊指數考慮資源的相對多度時,則可用結果解釋的信息量明顯增加。
(13)種間多元生態位重疊計測
生態位空間可以認為是多維空間的一條封閉的幾何曲線或是一個幾何面,在常態分配下,生態位的邊界在二維空間是一個機率橢圓,在三維空間是一個橢圓體,而多維空間則是多橢圓體。在典範對應分析中,一個種的機率橢圓代表著生態位寬度,其長度與標準差成比例(Pappas和Stoermer1997)。所以,生態位重疊實際上就是兩個種機率橢圓的重疊,它可以通過正態密度函式的指數求之。
生態位重疊值模型
建立在L-V方程基礎上的許多生態位模型,迄今已經產生了若干可檢驗的預測結果。生態位重疊值常常被用作L-V方程中競爭係數的估計。這種處理雖然可能較為方便,然而,將生態位重疊與競爭係數等同,可能值得懷疑並容易引起誤解。只有資源利用上的重疊,並不能保證會發生競爭,因為競爭依賴於可利用資源的數量和種群的大小。雖然生態位重疊是利用性競爭的一個必要條件,但重疊並不一定會導致競爭,除非資源供應不足。此外,干擾性競爭也不大可能形成,除非在對有限資源的利用過程中有發生重疊的可能,因此,避免競爭可能會導致資源利用模式的完全非重疊,即:間隔生態位(disjunctniche)。研究者生態位重疊本身對於干擾性競爭而言,既不是必要條件,也不是充分條件;而重疊對於利用性競爭而言,只是必要條件,而不是充分條件。許多事實證明:競爭與生態位重疊之間,經常可能是一種相反的關係。有關生態位重疊的假說認為:最大容許生態位重疊在強烈競爭的情況下,比在需求/供應比率相對較低的環境中要低。
有關生態位重疊的現有理論和模型,大多基於單個資源維度。很顯然,只有更多關注物種或種群間的多維生態位重疊,才能揭示出它們之間全面的生態關係。
生態位重疊的計測模型:曲線平均模型、對稱σ模型、非對稱σ模型、和σ法與積σ模型、似然估計模型、機率比模型、種間綴塊指數模型、方向性重疊計測模型、Morisita指數模型、積-矩相關係數模型、百分比重疊指數模型、映射函式法、集合論模型、生態位重疊間接計測模型(生態位分離計測模型、資源分離比率模型)、多種群生態位重疊模型、多維生態位計測模型。
例子
例子:1)歐亞紅松鼠(Eurasian Red Squirrel)在英國.,被灰松鼠(North American Grey Squirrel)替代了。因為在落葉林中紅松鼠消化榛子的能力低於灰松鼠。