基本介紹
與空間一點O有等距離R的點的全體,叫做球面。所有點都在同一球面上的圖形,叫做 球面圖形。
點O叫做球心,距離R叫做球的半徑,兩端點在球面上的線段,叫做球的弦。過球心的弦,叫做球的直徑,直徑的兩端點,叫做對徑點。
球面圖形的基本元素
用一平面去截球面,如果平面經過球心,那么,球面與平面的公共部分叫做大圓。如果平面不經過球心又與球面相交,那么,球面與平面的公共部分叫做小圓。
大圓與球面上的點是球面圖形的基本元素,它與平面圖形的點和直線相當,點與大圓有如下的關係。
1)通過任意給定的不是對徑的球面兩點有一大圓。
2)通過任意給定的不是對徑的球面兩點至多有一大圓。
3)若C₁與C₂是球面上任意兩個大圓,至少有一點是它們的交點。
4)每一大圓至少包含三個點。
5)若C是任一大圓,球面上至少有一點不屬於大圓C。
6)在球面上至少有一個大圓。
以上六個關係,如果不藉助球面外的任一點(如球心)可以把它們作為公理看待,如果藉助於球面外的任一點 (如球心),則以上關係可以證明,例如關係(3),過球心O的任意兩平面有公共點O,因而有公共直徑的兩端點,於是任意兩個大圓都通過它們公共直徑的對徑點。即是說在球面上沒有不相交的兩個大圓,現在利用球心來研究球面圖形 。
其他球面圖形及性質
定義2過球心的兩射線與球面相交於兩點A、B,兩點A、B與∠AOB內部的大圓部分叫做 大圓的劣弧。除劣弧外的大圓部分叫做這 大圓的優弧。顯然劣弧小於半大圓 。
 球面圖形
球面圖形定義3用大圓劣弧連線不在同一大圓上的球面三點A,B,C得一球面圖形,叫做 球面三角形。如圖1三點A、B、C叫做球面三角形的頂點,劣弧 叫做球面三角形的邊,有公共頂點的兩邊組成的角,叫做球面三角形的角,它的大小等於過頂點而切於兩弧的切線夾角。
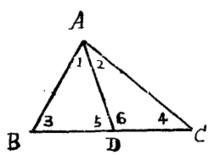 圖1
圖1與球面三角形相對應的有一個三面角。
如圖2,從球心O經球面三角形的三頂點A、B、C引射線,得到一個以球心為頂點的三面角O-ABC,這個三面角叫做球心三面角,三面角的三個面角對應於球面三角形的三邊,三面角的三個二面角對應於球面三角形的三內角。
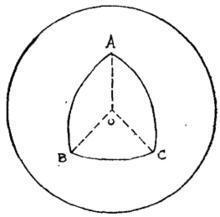 圖2
圖2定義4 垂直於大圓所在平面的直徑的兩個端點,叫做這個 大圓的極.
從定義4看出,大圓上任一點與它的極之間的大圓部分是這個大圓的1/4。
 球面圖形
球面圖形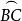 球面圖形
球面圖形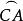 球面圖形
球面圖形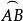 球面圖形
球面圖形設有球面三角形ABC,如圖3;邊的極分別為C',A',B',且點A’,A在的同側,點B'、B在的同側, 點C'、C在的同側, 則球面三角形A'B'C'叫做球面三角形ABC的 極三角形。
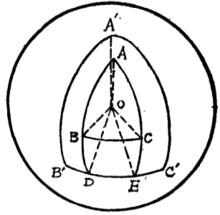 圖3
圖3定理1 若球面三角形A'B'C' 是球面三角形ABC的極三角形,則球面三角形ABC也是球面三角形A'B'C'的極三角形。
證明: 如圖3。
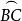 球面圖形
球面圖形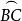 球面圖形
球面圖形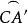 球面圖形
球面圖形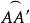 球面圖形
球面圖形(1)因為A'是 的極且與A在 的同側,所以 是大圓弧的,且 為劣弧。
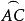 球面圖形
球面圖形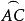 球面圖形
球面圖形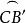 球面圖形
球面圖形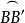 球面圖形
球面圖形(2)點B'是 的極且與B在 的同側,所以 是大圓弧的1/4,且 為劣弧。
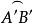 球面圖形
球面圖形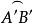 球面圖形
球面圖形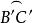 球面圖形
球面圖形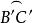 球面圖形
球面圖形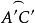 球面圖形
球面圖形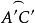 球面圖形
球面圖形由(1)、(2)知點C是 的極,且與C'在 的同側,同理點A是 的極,且與A'在 的同側。點B是 的極,且與B'在 的同側,故球面三角形ABC是球面三角形A'B'C'的極三角形。
(證畢) 。
定理2 球面三角形的角與它的極三角形的對應邊,就度量來說,它們互補。
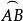 球面圖形
球面圖形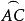 球面圖形
球面圖形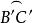 球面圖形
球面圖形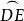 球面圖形
球面圖形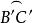 球面圖形
球面圖形證明:如圖3,延長與使分別交於D、E,則球面角∠A與的弧度數相同,要證明球面角∠A與邊 互補,只須證
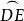 球面圖形
球面圖形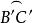 球面圖形
球面圖形+=1/2大圓=2直角
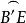 球面圖形
球面圖形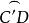 球面圖形
球面圖形1)∵=大圓,=1/4大圓
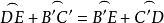 球面圖形
球面圖形2)∴=1/2大圓= 2直角
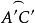 球面圖形
球面圖形3)同理,球面角∠B與互補
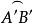 球面圖形
球面圖形球面角∠C與互補
(證畢)。
定理3 球面三角形三個內角的和,大於2直角而小於6直角。
證明: 設有球面三角形ABC,要證明∠A,∠B,∠C的和在2直角和6直角之間。
作球面三角形ABC的極三角形A'B'C',則從定理2得:
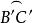 球面圖形
球面圖形1)∠A+= 2直角
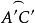 球面圖形
球面圖形∠B+= 2直角
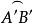 球面圖形
球面圖形∠C+= 2直角
2)以上三式兩邊分別相加得
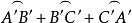 球面圖形
球面圖形∠A+∠B+∠C=6直角-()
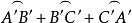 球面圖形
球面圖形3)由於0<<4直角
故:2直角<∠A+∠B+∠C<6直角。
(證畢) 。

