球面坐標系
 球面坐標變換
球面坐標變換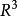 球面坐標變換
球面坐標變換 球面坐標變換
球面坐標變換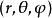 球面坐標變換
球面坐標變換定義. 設是中一點,在球面坐標系中的三個坐標變數是,其定義為
•徑向距離是從原點到點P的歐幾里得距離。
•傾角(或極角) θ是天頂方向和線段OP之間的夾角。
•方位(或方位角) φ是從方位參考方向到參照平面上線段OP的正交投影的有符號角度。
見右圖1。
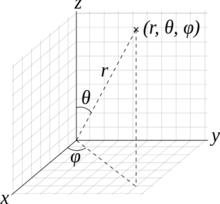 圖1
圖1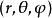 球面坐標變換
球面坐標變換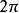 球面坐標變換
球面坐標變換與極坐標類似,球面坐標系相同的同一點,具有無限多個等效坐標,,你可以在不改變角度的情況下, 增加或減去任意數量倍的,從而不改變角點。在許多情況下,允許負徑向距離也很方便,,該慣例是(− r, θ, φ)等效於( r, θ+ 180 °, φ)為任意r,θ和φ。此外,( r,− θ, φ)等效於( r, θ, φ+ 180 °)。
如果需要為每個點定義一組唯一的球面坐標, 則必須限制它們的範圍。一個共同的選擇是:
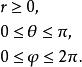 球面坐標變換
球面坐標變換球面坐標變換
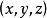 球面坐標變換
球面坐標變換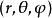 球面坐標變換
球面坐標變換球面坐標系是三大常用的坐標系之一,其它二個常用的坐標系是標準的歐氏坐標系、柱面坐標系。球面坐標變換公式描述了空間中一點P在歐氏坐標系下的坐標與球面坐標系下的坐標之間的變換關係。該變換關係如下述公式給出 :
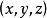 球面坐標變換
球面坐標變換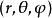 球面坐標變換
球面坐標變換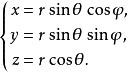 球面坐標變換
球面坐標變換或者,將表達成的形式:
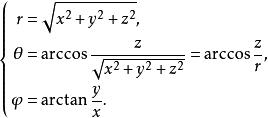 球面坐標變換
球面坐標變換體積元
在許多套用中,球面坐標系具有其它坐標系不具有的優點。了解在球面坐標系的面積元,體積元是對我們有幫助的。
長度元:
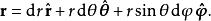 球面坐標變換
球面坐標變換其中
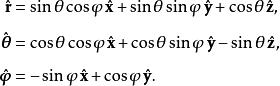 球面坐標變換
球面坐標變換面積元:
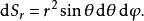 球面坐標變換
球面坐標變換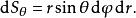 球面坐標變換
球面坐標變換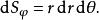 球面坐標變換
球面坐標變換體積元:
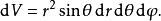 球面坐標變換
球面坐標變換梯度、散度、旋度以及Laplace運算元在球面坐標系下的由下述公式給出 :
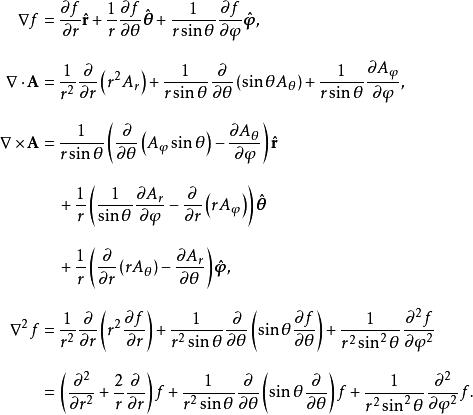 球面坐標變換
球面坐標變換