定義
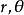 柱面坐標
柱面坐標 柱面坐標
柱面坐標 柱面坐標
柱面坐標 柱面坐標
柱面坐標 柱面坐標
柱面坐標 柱面坐標
柱面坐標 柱面坐標
柱面坐標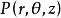 柱面坐標
柱面坐標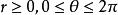 柱面坐標
柱面坐標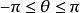 柱面坐標
柱面坐標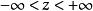 柱面坐標
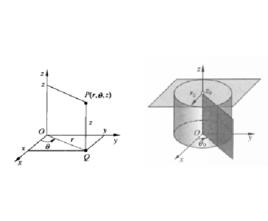
柱面坐標在空間直角坐標系中,任給一點P,設 是點 在 面上投影點的極坐標, 是點 的豎坐標,則稱 是點 的 柱面坐標(見圖1),記為 ,其中 (或 ), 。
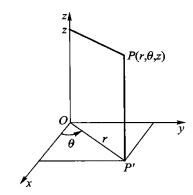 圖1
圖1求曲面的柱面坐標方程的方法
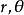 柱面坐標
柱面坐標 柱面坐標
柱面坐標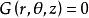 柱面坐標
柱面坐標求曲面的柱面坐標方程的方法與步驟,和求直角坐標方程類似,就是把曲面看作適合某種條件的點的集合或軌跡,將已知條件用曲面上點的柱面坐標 和 的關係式表示出來,就得到曲面的柱面坐標方程 。
柱坐標的坐標面
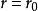 柱面坐標
柱面坐標 柱面坐標
柱面坐標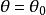 柱面坐標
柱面坐標 柱面坐標
柱面坐標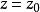 柱面坐標
柱面坐標 柱面坐標
柱面坐標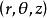 柱面坐標
柱面坐標特別地,方程 表示以 為軸的圓柱面; 表示過 軸的半平面; 表示垂直於 軸的平面,這三組面兩兩垂直,稱為 柱面坐標的坐標面,坐標面的交線稱為 坐標線。從圖2可知,空間每一點P總可看作位於某一母線平行於z軸的圓柱面上,並有三條坐標線(過P垂直於z軸的射線、平行於z軸的直線和圓心在z軸且與z軸垂直的圓周)通過,所以把 稱為點P的柱面坐標由此而來。
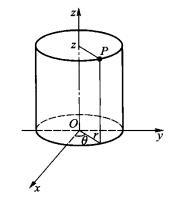 圖2
圖2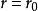 柱面坐標
柱面坐標當(常數)時,坐標面為柱面;
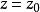 柱面坐標
柱面坐標當(常數)時,坐標面為平面;
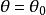 柱面坐標
柱面坐標當(常數)時,坐標面為半平面(見圖3).
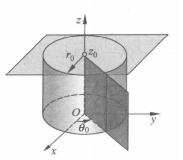 圖3
圖3柱面坐標變換
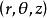 柱面坐標
柱面坐標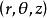 柱面坐標
柱面坐標空間中的任意點P的位置由3個參數 給出,其意義如圖2所示, 稱為柱面坐標。
從其與空間直角坐標系的關係得變換如下,此變換稱為 柱坐標變換。
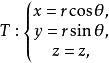 柱面坐標
柱面坐標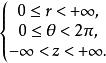 柱面坐標
柱面坐標其中
柱坐標的體積微元
柱坐標的體積微元由6個坐標面圍成。
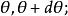 柱面坐標
柱面坐標(1)半平面
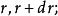 柱面坐標
柱面坐標(2)圓柱面
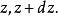 柱面坐標
柱面坐標(3)平面
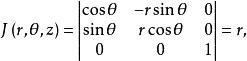 柱面坐標
柱面坐標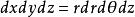 柱面坐標
柱面坐標由於 所以 見圖(4)。
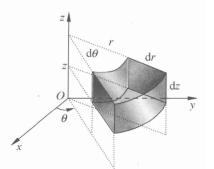 圖4
圖4柱坐標的換元公式
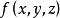 柱面坐標
柱面坐標如果 在V上連續,在變換
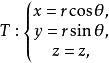 柱面坐標
柱面坐標其中
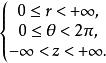 柱面坐標
柱面坐標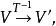 柱面坐標
柱面坐標下,有則
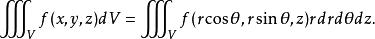 柱面坐標
柱面坐標值得注意的是,當r=0時,上面的公式亦成立.
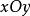 柱面坐標
柱面坐標在計算中,通常找出V在的投影區域D,即
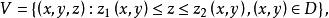 柱面坐標
柱面坐標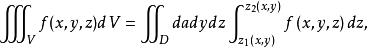 柱面坐標
柱面坐標從而得,然後在二重積分中利用極坐標變換即可.
化曲面的普通方程化為柱面坐標方程
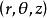 柱面坐標
柱面坐標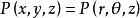 柱面坐標
柱面坐標設P點的柱面坐標為,點 滿足
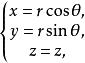 柱面坐標
柱面坐標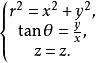 柱面坐標
柱面坐標或
利用上述公式,可以化曲面的普通方程化為柱面坐標方程:
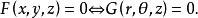 柱面坐標
柱面坐標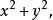 柱面坐標
柱面坐標一般來說,如果一個曲面以z軸為對稱軸,並且普通方程中含有 那么使用柱面坐標方程表示該曲面,可能會更簡單。
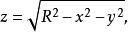 柱面坐標
柱面坐標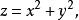 柱面坐標
柱面坐標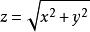 柱面坐標
柱面坐標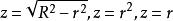 柱面坐標
柱面坐標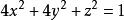 柱面坐標
柱面坐標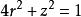 柱面坐標
柱面坐標例如,半球面旋轉拋物面 錐面 化為柱坐標方程分別為 。而橢球面 的柱面方程為 。