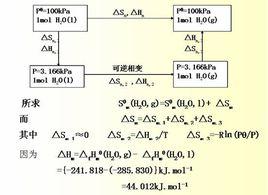
有關概念
1、熵:體系混亂度(或無序度)的量度。S表示熵。也表示黑洞中不可用熱量與其溫度的比值。
2. 熱力學第三定律:對於純物質的晶體,在熱力學零度時,熵為零。
3. 標準熵:1 mol物質在標準狀態下所計算出的標準熵值,用STP表示,單位:J·mol-1 ·K-1
計算公式
一般地,對於反應:mA + nB =xC + yD
DrSmq = 【x Sq,C + y Sq,D】– 【m Sq,A + n Sq,B】
1 可逆過程熵變的計算
根據克勞休斯數學表達式可知,如果兩平衡態間的過程是可逆的,熵變可用
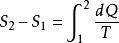 熵變
熵變求得(S1和S2分別表示系統在1態和2態的熵).可逆過程熵變可通過n摩爾理想氣體從初態
1(P1,V1,T1)變化到末態2(P2,V2,T2)求得.
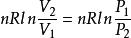 熵變
熵變(1)等溫過程 ΔS=
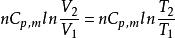 熵變
熵變(2)等壓過程 ΔS=
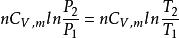 熵變
熵變(3)等容過程 ΔS=
(4)絕熱過程 ΔS=0.
(5)可逆循環過程 ΔS=0
2.不可逆過程熵變的計算
系統的熵僅與始末狀態有關,與過程無關,因此,若始、末兩態之間為一不可逆過程,則可以在兩態之間設計一個可逆過程,通過計算該可逆過程的熱溫比積分,得到系統在兩個平衡態之間不可逆過程的熵變.
2.1 絕熱自由膨脹過程
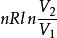 熵變
熵變絕熱自由膨脹過程是不可逆過程,該過程中氣體對外做功為零,從外界吸熱為零,內能增量為零,溫度不變,所以絕熱自由膨脹過程是一個等溫過程,即T1= T2.以n摩爾理想氣體從初態1(P1,V1,T1)經絕熱自由膨脹過程變化到末態2(P2,V2,T2)為例。ΔS=
2.2 物質混合過程
以質量為m1、溫度為T1的冷水,與質量為m2、溫度為T2的熱水接觸達到熱平衡為例,討論二者的總熵變(設熱傳導過程中冷、熱水系統與外界均無熱交換,水的比熱為c).由於系統與外界沒有能量和物質的傳遞和交換,所以系統可看成是孤立系統,求總熵即為求系統的熵變.系統在混合過程中,從外界吸收的熱量為零,但系統熵變並不為零,所以水溫由不均勻到達均勻的過程實際是一個不可逆過程.計算水的熵變(為計算混合前後水的熵變,可假設水的混合過程是可逆的等壓過程).
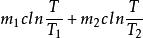 熵變
熵變ΔS=
2.3 等壓熱傳導過程
以絕熱真空容器中兩個完全孤立的不同溫度物體經熱接觸後達到熱平衡為例,討論系統的總熵變.系統與外界沒有能量和物質的交換和傳遞,所以該系統可看作為孤立系統,兩物體經熱接觸後達到熱平衡的過程為不可逆過程,壓強不變,故在接觸前後建立一個等壓可逆過程來求解系統的熵變.
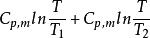 熵變
熵變ΔS=
求解熵變應注意的兩個問題
(1)判別熱力學過程是否可逆是解決問題的關鍵.若為可逆過程,直接用上面給出的公式求解;若為不可逆過程,必須明確不可逆過程中不變的狀態參量,然後設計一個該狀態參量恆定的可逆過程求解熵變.
(2)若要完整地求解熵變問題,必須熟練掌握各可逆過程中的過程方程、邁耶公式、比熱容等常用表達式.
影響因素
1)熵變(ΔS)與體系中反應前後物質的量的變化值有關:
a. 對有氣體參加的反應:
 熵變
熵變主要看反應前後氣體物質的量的變化值即Δn(g),Δn(g)正值越大,反應後熵增加越大;Δn(g)負值越大,反應後熵減越多;
b. 對沒有氣體參加的反應:
主要看各物質總的物質的量的變化值即Δn(總),Δn(總)正值越大,熵變正值越大;Δn(總)負值絕對值越大,熵變也是負值的絕對值越大,但總的來說熵變在數值上都不是特別大.
2)熵變(ΔS)值隨溫度的改變變化不大,一般可不考慮溫度對反應熵變(ΔS)的影響.
3)熵變(ΔS)值隨壓力的改變變化也不大,所以可不考慮壓力對反應熵變的影響.
關係
對於孤立體系而言,在其中發生的任何反應變化必然是自發的。熱力學第二定律告訴我們:在孤立體系中發生的任何變化或化學反應,總是向著熵值增大的方向進行,即向著△S孤立0的方向進行的。而當達到平衡時△S孤立=0,此時熵值達到最大。
假如不是孤立體系,則可以把體系與其四周的環境一起作為一個新的孤立體系考慮,熵增原理仍然是適用的。由此可以得出,自發反應是向著0的方向進行的。大家知道,在常壓下,當溫度低於273K時,水會自發地結成冰。這個過程中體系的熵是減小的,似乎違反了熵增原理。但應注重到,這個體系並非孤立體系。在體系和環境間發生了熱交換。從水變成凍的過程中體系放熱給環境。環境吸熱後熵值增大了,而且環境熵值的增加超過了體系熵值的減小。因而體系的熵變加上環境的熵變仍是大於零的,所以上述自發反應是符合熱力學第二定律的。
熱力學第二定律:孤立體系(絕熱體系)的自發過程是體系熵增加的過程,即:
狀態ISI表示; 狀態II用SII表示,所以 DS = SII - SI
DS > 0,過程自發進行;
DS < 0,逆過程自發進行;
DS = 0,平衡狀態