簡介
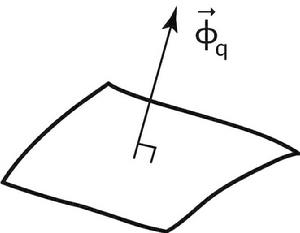
熱通量(英語:heat flux),又稱為 熱流,是指單位時間通過某一面積的熱能,是具有方向性的矢量,其在國際單位制中的單位為焦耳/秒(J/s,即瓦特)。由此又可以進一步定義 熱通量密度或 熱流密度,即通過單位面積的熱通量,其在國際單位制的單位為瓦特/平方米(W/m )。
熱傳導
熱傳導,是熱能從高溫向低溫部分轉移的過程,是 一個分子向另一個分子傳遞振動能的結果。各種材料的熱傳導性能不同,傳導性能好的,如金屬,還包括了自由電子的移動,所以傳熱速度快,可以做熱交換器材料,而金屬傳導能力依次為銀>銅>金>鋁;傳導性能不好的,如石棉,可以做熱絕緣材料。
傅立葉定律
熱傳導定律,也稱為傅立葉定律,描述了熱量在介質中的傳導規律。其形式與電傳導歐姆定律相似。 傅立葉定律可以以兩種形式表述:微分形式關注於局部的能量傳導率,而積分形式則關注於流入和流出整體一部分介質的能量。
微分形式
傅立葉定律的微分形式表明了熱通量密度正比於熱導率乘以負的溫度梯度。熱通量密度是單位時間內流過單位面積的熱量。
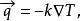 熱流單位
熱流單位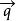 熱流單位
熱流單位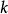 熱流單位
熱流單位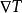 熱流單位
熱流單位這裡(使用國際單位制): 是熱通量密度,單位W·m, 是這種材料的熱導率,單位W·m·K, 是溫度梯度,單位K·m。
熱導 k通常情況下都被當作是常數,但是實際情況是, k的值會隨溫度而變化。而然在很大的溫度範圍內, k的變化都可忽略不計。在各向異性介質中,熱導率顯著地隨方向而變化,這時 k是一個二階張量。在非均勻介質中, k與空間位置有關。
在許多情況下,當我們只需考慮一個方向上的熱傳遞(比如x方向)時,可用一維傅立葉定律:
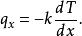 熱流單位
熱流單位積分形式
通過在部分介質表面 S上對微分式進行積分,我們得到了傅立葉定律的積分形式:
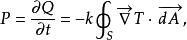 熱流單位
熱流單位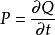 熱流單位
熱流單位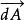 熱流單位
熱流單位這裡(使用國際單位制): 是熱傳導功率,即單位時間通過面積 S的熱量,單位W,而 是面元矢量,單位m。
當我們所研究的介質是一段兩端溫度恆定、均勻的一維介質時,積分得到的熱傳導功率為:
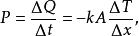 熱流單位
熱流單位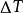 熱流單位
熱流單位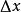 熱流單位
熱流單位這裡 A是介質的截面積, 是兩端溫差, 是兩端距離。
這一定律是熱傳導方程式的基礎。
化工方面的套用
幾乎各種化學工業都有熱交換過程,需要熱交換器,而根據熱傳導的方式和工藝要求,設計各種熱交換器。
相關條目
•熱導率
•熱傳
•熱對流
•熱輻射