定義
拓撲空間(X,τ),A⊆X,稱A是 無處稠密的(亦稱 稀疏的,或稱A為 無處稠密集、 稀疏集),若且唯若A的閉包的內部是空集。
例子
例如,整數在實數軸 R上就形成了一個無處稠密集。
注意運算的次序是很重要的。例如,有理數的集合,由於是 R的子集,因此它的內部的閉包(注意不是“閉包的內部”)是空集,但不是無處稠密集;實際上,它在 R上是稠密的,正好相反。
無處稠密與周圍的空間也有關:有可能把一個集合考慮為 X的子空間時就是無處稠密的,但考慮為 Y的子空間時,就不是無處稠密的。顯然,一個集合在它本身中總是稠密的。
開集和閉集
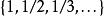 無處稠密集
無處稠密集一個無處稠密集不一定是閉集(例如,集合在實數集上是無處稠密集),但一定是包含在一個無處稠密的閉集(即它的閉包)內。確實,一個集合是無處稠密集,若且唯若它的閉包是無處稠密集。
無處稠密的閉集的補集是一個稠密的開集,因此無處稠密集的補集是內部為稠密的集合。
測度為正數
一個無處稠密集並不一定就是可忽略的。例如,如果 X位於單位區間[0,1],不僅有可能有勒貝格測度為零的稠密集(例如有理數集),也有可能有測度為正數的無處稠密集。
例如(一個康托爾集的變體),從[0,1]內移除所有形為 a/2 的最簡二進分數,以及旁邊的區間[ a/2 −1/2 , a/2 +1/2 ];由於對於每一個 n,這最多移除了總和為1/2 的區間,留下的無處稠密集的測度就至少是1/2(實際上剛剛大於0.535……,因為重疊的原因),因此在某種意義上表示了[0,1]的大多數空間。
把這個方法進行推廣,我們可以在單位區間內構造出任意測度小於1的無處稠密集。
參見
•貝爾空間
•史密斯-沃爾泰拉-康托爾集
