無粘性不可壓縮流體動力學
正文
流體動力學中主要研究無粘性不可壓縮流體在繞過物體時的流動和管內流動規律的一個分支，又稱經典流體動力學。這一學科分支的任務是求解流場中的速度、壓力分布和物體受力。它忽略了真實流體的粘性和壓縮性，也不考慮表面張力，從而大大簡化了複雜的流體動力學問題，故常作為近似處理許多工程問題的依據。速度勢方程 許多無粘性不可壓縮流體的流動，如來流均勻或流體從靜止開始的流動，均為無旋流動。無旋流動時存在速度勢嗞，相應的速度勢方程為:
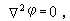式中
為拉普拉斯運算元,在直角坐標系中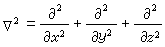 
利用這一方程和給出的邊界條件就可解出嗞；再由 
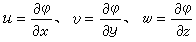可得到流場速度分布，u、v、w 分別為x、y、z方向的速度分量。 柯西積分 歐拉方程在重力場中無旋流動條件下的線積分。它可敘述為：同一時刻流場中任意兩點上的值
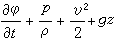相等。p為壓力，
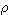為密度，v為速度模，g為重力加速度，z為距參考水平面的高度。利用柯西積分可確定流場中的壓力分布；由此再沿物面積分可得到流體作用於物面的合力。 流函式 不可壓縮流體平面流動時存在流函式
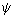，其)定義為:
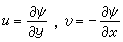。u、v為速度分量。流函式有以下性質：①等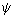線是流線；②任意兩條等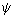線構成一個流管（見流體運動學），其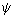值之差就是該流管中單位寬度通過的體積流量；③無旋流動時等 嗞線與等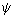線正交。 行動網路圖 流場中等 嗞線與等
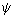線組成的正交網路（見圖）。由行動網路圖可看出流動圖案即流譜，並能估算流場中各點速度的大小和方向。對於平面流動相鄰兩條流線構成的小流管中單位寬度,通過的體積流量為△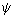=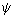1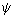－2；等嗞線被割截的弧長Δn 就是該流管單位寬度的截面積，於是該流管各截面上的平均流速
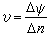該流管中心線沿流動的方向即為速度方向。 
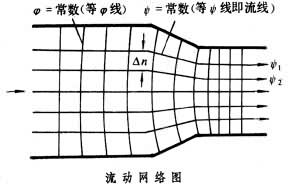無粘性不可壓縮流體動力學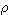v
Γ。這個公式稱為庫塔-儒科夫斯基升力定理。式中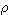為密度；vΓ為來流速度；Γ為速度環量,它是速度v沿包圍物體的封閉曲線l的線積分,即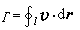
。 參考書目
V. L. Streeter, Fluid Mechanics, 5th ed.,McGraw-Hill,New York,1971.
