邊界層理論
正文
當流體在大雷諾數條件下運動時,可把流體的粘性和導熱看成集中作用在流體表面的薄層即邊界層內。根據邊界層的這一特點,簡化納維-斯托克斯方程,並加以求解,即可得到阻力和傳熱規律。這一理論是德國物理學家L.普朗特於1904年提出的,它為粘性不可壓縮流體動力學的發展創造了條件。邊界層 流體在大雷諾數下作繞流流動時,在離固體壁面較遠處,粘性力比慣性力小得多,可以忽略;但在固體壁面附近的薄層中,粘性力的影響則不能忽略,沿壁面法線方向存在相當大的速度梯度,這一薄層叫做邊界層。流體的雷諾數越大,邊界層越薄。從邊界層內的流動過渡到外部流動是漸變的, 所以邊界層的厚度δ通常定義為從物面到約等於99%的外部流動速度處的垂直距離,它隨著離物體前緣的距離增加而增大。根據雷諾數的大小,邊界層內的流動有層流與湍流兩種形態。一般上游為層流邊界層,下游從某處以後轉變為湍流,且邊界層急劇增厚。層流和湍流之間有一過渡區。當所繞流的物體被加熱(或冷卻)或高速氣流掠過物體時,在鄰近物面的薄層區域有很大的溫度梯度,這一薄層稱為熱邊界層。
分析方法 大雷諾數的繞流流動可分為兩個區,即很薄的一層邊界層區和邊界層以外的無粘性流動區。因此,處理粘性流體的方法是:略去粘性和熱傳導,把流場計算出來,然後用這樣的初次近似求得的物體表面上的壓力、速度和溫度分布作為邊界層外邊界條件去解這一物體的邊界層問題。算出邊界層就可算出物面上的阻力和傳熱量。如此的疊代程式使問題求解大為簡化,這就是經典的普朗特邊界層理論的基本方法。
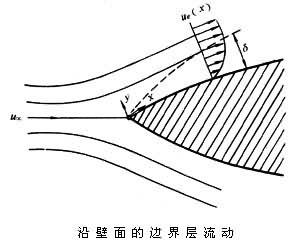
邊界層方程組 不可壓縮流體在大雷諾數的層流情況下繞過平滑壁面的情況(見圖)。沿物體壁面的方向為x軸,垂直於壁面的方向為y軸。由於邊界層厚度δ比物面特徵尺寸L小得多,因此對二維的忽略體積力的納維-斯托克斯方程逐項進行數量級分析,在忽略數量級小的各項後,可近似認為邊界層垂直方向的壓力不變,從而得到層流邊界層方程組為
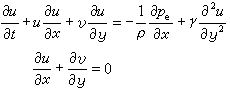
y=0處 u=0 v=0
y→∞處u=ue(x,t)
式中pe為主流在邊界層外緣上的壓力,pe=f(x,t);ρ為流體密度;u、v代表x、y方向的速度分量;t為時間。
 邊界層理論
邊界層理論