準穩電磁場
正文
忽略推遲效應,也就是忽略波的傳播,它相應於位移電波的效應可以略去的情況(與傳導電流相比)。這就是準穩場的條件,但此條件也允許有局部的例外,這種局部的例外區就是電容區(如電容器內部)。在電容區內,位移電流不可忽略,但電場主要是庫侖場,渦旋電場可以略去不計。在均勻介質內部,當自由電荷體密度為零時,如採用國際單位制,準穩場滿足擴散方程
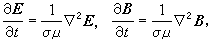 (1)
(1)
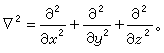
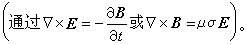
在真空或絕緣介質中,σ=0。因此場滿足的方程(1)化為拉普拉斯方程
 (2)
(2)
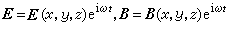 ,這時擴散方程化為亥姆霍茲方程
,這時擴散方程化為亥姆霍茲方程  (3)
(3)
由於導體中電磁波的波長比其在真空中波長小得多,因此在粗導線情況,導線的橫向尺寸比起導體中電磁波波長不一定小,這時導線中的電流(以及電磁場)的分布將集中在表面附近,這就是趨膚效應。在趨膚效應顯著的情況,導線內的電流和電磁場的分布將和穩恆情況有很大不同。穩恆時(ω=0),在導體內部也像在空氣中一樣滿足拉普拉斯方程。
從亥姆霍茲方程解出圓柱形直導線上的電流分布為
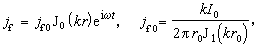 (4)
(4)
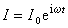 ),
), 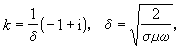 (5)
(5)
當頻率足夠低,使得δ
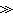 r0成立時,式(4)可近似化為
r0成立時,式(4)可近似化為 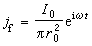 , (6)
, (6)
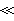 r0時,在r
r0時,在r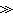 δ處,式(4)近似化為
δ處,式(4)近似化為 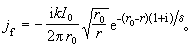 (7)
(7)
單位長度導線的表面阻抗ZS的定義為表面電場E(r0)與總電流I0的比
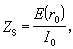 (8)
(8)
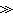 r0情況,
r0情況,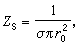 即為單位長度上的直流電阻。而在δ
即為單位長度上的直流電阻。而在δ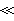 r0時,
r0時, 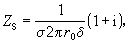 (9)
(9)
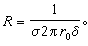 (10)
(10)
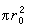 降到2πr0δ。電感分量為
降到2πr0δ。電感分量為 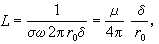 (11)
(11)
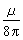 小。
小。 同樣,由於高頻電流分布與直流的不同,線圈的高頻電感(包括外電感)和高頻電阻亦將與直流的值不一樣。高頻電阻和高頻電感也可以通過焦耳熱和磁能來計算
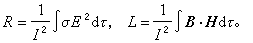 (12)
(12)
在準穩情況,一個電路上的總電流I可用集中參數的電路方程來確定(見電路),但在頻率較高使得導線橫向尺寸大於或相當於電磁波在導體中的趨膚厚度時,電路的電感和電阻要採用相應頻率時的值。
非定頻的擴散方程(1)在實際中亦有套用。如磁場的擴散在許多領域中都是一個重要效應。η=1/σ μ稱為擴散率,σ μ 愈大,擴散就愈慢。由於這種擴散效應,導體中若原有磁場,則該磁場將隨時間而衰減。對於實驗室中的導體,擴散時間τ一般較小,銅是電導率很大的導體,可是對1厘米半徑的銅球,τ也只有10-2秒。但若導體大小達到天體的線度時,則τ可以達到很大的值。例如太陽中的磁場,τ可達1010年。