簡述
洛倫茨吸引子及其導出的方程組是由愛德華·諾頓·洛倫茨於1963年發表,最初是發表在《大氣科學雜誌》( Journal of the Atmospheric Sciences)雜誌的論文《 Deterministic Nonperiodic Flow》中提出的,是由大氣方程中出現的對流卷方程簡化得到的。
這一洛倫茨模型不只對非線性數學有重要性,對於氣候和天氣預報來說也有著重要的含義。行星和恆星大氣可能會表現出多種不同的準周期狀態,這些準周期狀態雖然是完全確定的,但卻容易發生突變,看起來似乎是隨機變化的,而模型對此現象有明確的表述。
從技術角度看來,洛倫茨振子具有非線性、三維性和確定性。2001年,沃里克·塔克爾(Warwick Tucker)證明出在一組確定的參數下,系統會表現出混沌行為,顯示出人們今天所知的奇異吸引子。這樣的奇異吸引子是豪斯多夫維數在2與3之間的分形。彼得·格拉斯伯格(Peter Grassberger)已於1983年估算出豪斯多夫維數為2.06 ± 0.01,而關聯維數為2.05 ± 0.01。
此系統也會出現在單模雷射和發電機的簡化模型中。 除此之外,閉環對流、水輪轉動等物理模型也有此系統的套用。
洛倫茨吸引子是 洛倫茨振子(Lorenz oscillator)的長期行為對應的分形結構,以愛德華·諾頓·洛倫茨的姓氏命名。洛倫茨振子是能產生混沌流的三維動力系統,是一種吸引子,以其雙紐線形狀而著稱。映射展示出動力系統(三維系統的三個變數)的狀態是如何以一種複雜且不重複的模式,隨時間的推移而演變的。
洛倫茨方程
洛倫茨方程是基於納維-斯托克斯方程、熱傳導方程和連續性方程簡化得出,最初的形式為:
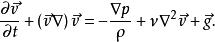 洛倫茨吸引子
洛倫茨吸引子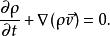 洛倫茨吸引子
洛倫茨吸引子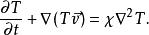 洛倫茨吸引子
洛倫茨吸引子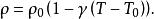 洛倫茨吸引子
洛倫茨吸引子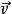 洛倫茨吸引子
洛倫茨吸引子 洛倫茨吸引子
洛倫茨吸引子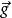 洛倫茨吸引子
洛倫茨吸引子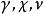 洛倫茨吸引子
洛倫茨吸引子——流速,T——流體溫度,T——上限溫度, ——密度,p——壓強, ——重力, ——依次為熱膨脹係數、熱擴散率和動黏滯係數。
簡化後的形式稱為 洛倫茨方程,是決定洛倫茨振子狀態的方程為一組常微分方程:
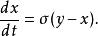 洛倫茨吸引子
洛倫茨吸引子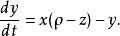 洛倫茨吸引子
洛倫茨吸引子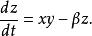 洛倫茨吸引子
洛倫茨吸引子含時間參數的形式:
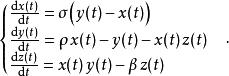 洛倫茨吸引子
洛倫茨吸引子 洛倫茨吸引子
洛倫茨吸引子 洛倫茨吸引子
洛倫茨吸引子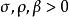 洛倫茨吸引子
洛倫茨吸引子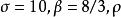 洛倫茨吸引子
洛倫茨吸引子稱為 普蘭特爾數,稱為 瑞利數。所有的,但通常不定。
瑞利數
| 不同ρ值時的洛倫茨吸引子 | |
| ρ=14, σ=10, β=8/3(放大) | ρ=13, σ=10, β=8/3(放大) |
| ρ=15, σ=10, β=8/3(放大) | ρ=28, σ=10, β=8/3(放大) |
| ρ值較小時,系統是穩定的,並能演變為兩個定點吸引子中的一個;當ρ大於24.74時,定點變成了排斥子,會以非常複雜的方式排斥軌跡,演變時自身從不交叉。 | |
原始碼
GNU Octave
下面是GNU Octave模擬洛倫茨吸引子的原始碼:
Borland C
參見
•混沌映射列表
•Takens定理
•曼德布洛特集合
