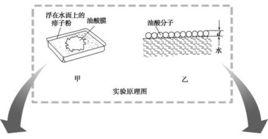
油膜法理解障礙
⑴借比法理解"油膜法"的原理.
⑵模型法理解物質的微觀結構.
物理上有許多模型,它可分為:①物體模型,如質點,恆壓電源等;②狀態模型,如靜止,勻速運動等;③過程模型,如氣體的等溫過程等.物理上的"理想模型",就是為了便於研究問題而建立的一種高度抽象的理想客體或理想過程."理想模型"是現實世界中找不到的東西,但是,"理想模型"是以客觀實在為原型的,是對客觀事物或過程的一種近似反映,它突出反映了客觀事物或過程的某一主要矛盾或主要特性,完全忽略了其他方面的矛盾或特性.物理學中創建的"理想模型",叫做"物理模型",也簡稱模型.運用"理想模型"及其理論解決問題的方法就是模型法.
物質微觀結構的三種理想模型分別是:①把分子視為球形模型[V分=4π(d/2) 3/3=πd3/6];②把分子視為立方體模型(V分=d3);③每個氣體分子位於相同一個立方體的中心模型(圖11—1—1,把氣體分子理想地假設為:分子均勻分布,並且每個分子所占有的空間為相同的正立方體,氣體分子在立方體的中心.分子的平均間距等於正立方體的邊長L,即d=L).
油膜法解題障礙
微觀量的計算,一般要用油膜法和估算法.計算微觀量,一般要涉及巨觀量和阿伏加德羅常數.
⑴油膜法求分子的直徑.
將油膜視為單分子油膜,不考慮各油分子間的間隙,油膜分子視為球形,油分子的直徑等於油膜厚度.油分子的直徑
d=
[例1]將1 cm3的油酸溶於酒精,製成200 cm3的油酸酒精溶液.已知1 cm3的溶液有50滴,現取1滴油酸酒精溶於水,油酸在水面上形成一單分子薄層,已測出這一薄層的面積為0.2 m2,由此可估算油酸分子的直徑為_______m.
解析:1滴油酸酒精溶液中油酸體積V=(10^-6 m^3/50)*(1 cm^3/200 cm^3)=10^-10 m^3,則油酸分子的直徑d=V/S=5×10^-10 m.
點評:除油膜法計算分子大小外,如果在已知分子的體積V的情況下,對固體,液體還有方法:①當分子視為球體時,有V=4π(d/2)3/3=πd3/6,d=;②當分子視為立方體時,d=.對氣體,因分子的間距很大,不考慮氣體分子的大小.
⑵估算法求微觀量.
估算是從已知條件出發,運用與題設條件密切相關的物理概念,規律和常數,對要求的問題作出合理的科學的估算的思維方法.
[例2]一熱水瓶中水的質量約為2.2 kg,它所包含的水分子數目約為______(取二位有效數字,阿伏加德羅常數取6.02×1023 mol-1).
解析:水的摩爾質量M=18×10-3 kg/mol,則2.2 kg水所含水分子數N=(m/M)NA=7.3×1025.
點評:解估算題的依據,就是一些物理理論,公式和一些常數,常識等.本節估算題常用的理論依據:對固體,液體而言,分子體積V分=V(物質體積)/N(分子總數),其中V=m(物質質量)/ρ(密度);VA(摩爾體積)=M(摩爾質量)/ρ;某物質的分子數N=nNA=(m/M)NA=(V/VA)NA.若物質是氣體,則VA=22.4 L,當未給V的壓強和溫度時,則把V就近似認為是標準狀況下的體積.d(分子直徑)=V(油滴體積)/S(單分子油膜面積).常數或常識有阿伏加德羅常數,摩爾質量等.
油膜法學習重點
本節的重點是掌握油膜法粗測分子的大小,記住一般分子直徑的數量級,能根據巨觀量和阿伏加德羅常數計算微觀量.本節常見的題型為選擇題,定性分析較多,定量計算較少. 命題熱點是粗測分子大小的油膜法.
油膜法測分子直徑的模擬實驗
在高中物理的熱運動一章中曾講到分子大小的粗略測定方法——油膜法。其原理是測出一滴油珠的直徑D,根據公式V=1/6πD^3求出這滴油珠的體積,把這一滴油珠滴在較大水面上,使其面積儘量擴散開,當擴散成單分子層油膜時,測出油膜的面積S,然後用公式 d=V/S求出油膜的厚度d。因為是單分子層,所以油膜的厚度也就是油分子的直徑。
油膜法測分子大小的實驗,在學校是不易做到的。例如,直徑為5mm油滴,把它滴在水面上,若擴散成單分子層油膜,其面積大約是1.2×103m,相當於邊長是34.5m的正方形的面積。如此大的水面,一般的學校是無法做到的。因此,學生也就無法獲得油膜法測分子大小的感性認識。
為了加深對油膜法測分子大小實驗方法的理解,我在教學中,給學生安排了一次模擬實驗。方法是用小口徑量筒量得20ml小m,倒在一張八開紙上,把小m攤開成一層,用刻度尺測出小m的面積S,然後計算出小m層的厚度,也就是小m的直徑了。實驗時,量小m體積的量筒用小口徑的(例如口徑是10mm)為好,量得小m的體積比較精確。
做實驗時,發現許多學生都用學生尺慢慢地把小m推攏成一個矩形,再測它的面積。這樣做當然測得的面積值是比較準確些,但作為油膜法的模擬,這種有意把小m推攏成矩形側面積的做法是不科學的,因為油膜不會擴散成規則的幾何形狀。正確的做法是在攤開小m的過程中,把小m攤成任意形狀的平面,如圖中虛線所示,當然儘可能讓小m一顆挨一顆。然後按圖中實線所示的矩形測得近似的面積S,再計算出小m的厚度。這次實驗,各小組測得小m的直徑約在1.14mm~1.31mm之間。在學生做實驗的同時,我用遊標卡尺測了六顆小m的直徑,約在1.26mm~1.32mm之間。
如果仔細觀察一下小m的形狀可以發現,小m是扁圓形的,把小m攤成單層以後,絕大多數小m都成平放狀態,很少是豎立起來的;再者,小m是固體,沒有流動性,在自然攤成任意形狀平而的情況下,不易真正做到所有小m都是一顆挨一顆的,由於這些因素,把小m攤成平面面積比真實單層小m平均面積稍大,求得單層小m厚度比真實平均厚度稍小。若用油菜籽做這個實驗,效果會更好些。