起重機大車的水平側向力
在橋式類型起重機大車運行跑偏時,軌道側面與車輪輪緣或水平導向輪之間會產生水平側向力。
水平側向力對起重機車輪及其軸承有著不良影響,側向力通過起重機軌道作用於廠房結構。
水平側向力可按照下式近似計算:
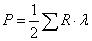 水平側向力
水平側向力式中 ∑ R----起重機產生側向力一側最大輪壓之和;
λ---水平側向力係數,與起重機跨度和大車輪距之比有關。
考慮剛度變化的 Pushover 水平側向力分布
為了考慮層間剛度對豎向不規則結構非線性靜力分析結果的影響,提出了建築結構考慮剛度變化的水平側向力分布計算方法。在總結幾種常見水平側向力分布形式、分析單自由度體系運動方程的基礎上,給出了單自由度、多自由度體系水平地震力與層間剛度的關係,提出了改進的水平側向力分布形式。算例計算表明,可以找到多種側向剛度不規則結構的薄弱層,得到的樓層側移和層間位移角與時程分析結果符合較好。
均勻分布
該方法認為沿建築物高度側向力均勻分布,每一層的側向力和該層的質量成正比。每一層的水平側向力 F可由下式計算:
F=αW式中, α為比例係數, W為第 i樓層的重力荷載代表值。
水平側向力均勻分布形式過於簡單,只考慮了樓層質量對地震作用的影響,而沒有考慮結構剛度、強度以及振型等參數對非線性分析結果的影響,計算結果與實際結構反應有較大的差異。
MMC 法分布
E· kalkan和S·K· Kunnath考慮振型的影響,提出了MMC水平側向力分布形式:
F=∑ α Γ mφ S ( ζ , T )
式中, α為修正係數,可正可負; φ為 n振型向量。
MMC分布形式實際為各振型對地震力貢獻的線性組合,該方法雖然考慮多振型的影響,理論上也可以用於不規則結構,但是由於係數αn的不確定性,包括正負號的不確定,導致在具體計算時,要對各種可能出現的組合分別計算,並取其包絡線作為最終結果,特別是在考慮多階振型時,計算過程十分複雜。
除了上述水平側向力分布形式,常見的還有按照結構第一振型分布的側向力,以及其他按照結構某幾個振型進行組合 ( 例如,SRSS組合方法)的分布形式。筆者通過計算比較,認為如果側向力分布按照多個振型的組合形式分布,雖然得到的結果可以接受,但是計算過程還是偏於複雜,不利於實際工程套用。
考慮剛度變化的水平側向力分布
豎向不規則結構和規則結構的一個顯著區別就是側向剛度有較大的突變,可見,豎向不規則結構在進行pushover分析時,必須考慮其剛度變化的特點,其水平側向力分布也應該考慮剛度的影響。
在水平地震作用下質點的慣性力和質量成正比,這也就是pushover分析水平側向力均勻分布的原因了。若忽略阻尼的影響,則質點慣性力與剛度也是成正比的。對於多自由度體系也可以得到同樣的結論。層間剛度大則承受的水平地震力就越大,反之,亦然。在此,引入層間剛度對傳統的水平側向力分布進行修正,使其符合豎向不規則結構在地震作用下的水平慣性力分布。
非線性靜力推覆分析的水平側向力
非線性靜力分析方法可以較為簡便地預估結構的彈塑性反應,但僅取常見水平側向力分布模型並不能滿足實際工程的需要,例如高振型的影響和不規則結構的特殊性。對豎向不規則結構進行非線性時程分析,建立了水平側向力分布與結構層剛度的關係式,從而提出了一種新的水平側向力分布形式和方法。
幾種水平側向力分布形式
1、均勻分布
側向力沿建築物高度均勻分布,每一層的側向力和該層的質量成正比。只考慮了樓層質量對地震作用的影響,而沒有考慮結構剛度、強度以及振型等參數對非線性分析結果的影響,計算結果與實際結構反應有較大的差異,只是一種近似粗略的非線性分析方法。
2、指數分布
為了說明不同樓層加速度的變化,需要考慮變形的不同模態以及振動時高振型的影響,FEMA-356推薦使用指數分布形式。
指數分布雖然考慮了振型的影響,其中,倒三角分布只考慮了第一振型的貢獻,但是其分布形式含有假定結構的反應與其等效單自由度體系的反應相聯繫的意思,與多自由度體系的實際受力狀態還是有一定的差別,且權函式的取值也有商榷之處。
不規則結構的水平側向力分布
對5種不規則結構進行非線性時程分析,得到各層的加速度反應值 S,考慮各層的質量,從而求出各層水平地震慣性力 F(取7條地震波時程分析結果的平均值),然後利用各層側向剛度 D,作出水平地震慣性力和側向剛度關係曲線,並進行二次曲線擬合分析,得到剛度不規則結構水平側向力分布形式:
Δ F=(16.546 -3.031 D +0.175 D )Δ V
式中, D為各層側向剛度,計算方法參照框架結構側移計算的 D值法,Δ V為基底剪力增量。