演算發展
在20世紀80年代中期,很多學者開始對點集數據的配準進行了大量研究。1987年,Horn、Arun等人用四元數法提出點集對點集配準方法。這種點集與點集坐標系匹配算法通過實踐證明是一個解決複雜配準問題的關鍵方法。1992年,計算計視覺研究者Besl和Mckay介紹了一種高層次的基於自由形態曲面的配準方法,也稱為疊代最近點法ICP(Iterative Closest Point)。以點集對點集(PSTPS)配準方法為基礎,他們闡述了一種曲面擬合算法,該算法是基於四元數的點集到點集配準方法。從測量點集中確定其對應的最近點點集後,運用Faugera和Hebert提出的方法計算新的最近點點集。用該方法進行疊代計算,直到殘差平方和所構成的目標函式值不變,結束疊代過程。ICP配準法主要用於解決基於自由形態曲面的配準問題。
疊代最近點法ICP最近點法經過十幾年的發展,不斷地得到了完善和補充。Chen和Medioni及Bergevin等人提出了point-to-plane搜尋最近點的精確配準方法。Rusinkiewicz和Levoy提出了point-to-p rojection搜尋最近點的快速配準方法。Soon-Yong和Murali提出了Contractive-projection-point搜尋最近點的配準方法。此外,Andrew和Sing提取了基於彩色三維掃描數據點紋理信息的數據配準方法,主要在ICP算法中考慮三維掃描點的紋理色彩信息進行搜尋最近點。Natasha等人分析了ICP算法中的點雲數據配準質量問題。
基本原理
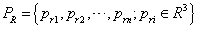 ICP算法
ICP算法三維空間R3存在兩組含有n個坐標點的點集PL和PR,分別為: 和(0-1)。三維空間點集PL中各點經過三維空間變換後與點集PR中點一一對應,其單點變換關係式為:
上式中,R為三維鏇轉矩陣,t為平移向量。
在ICP配準方法中,空間變換參數向量X可表示為[9] 。參數向量中四元數參數滿足約束條件為:
(0-2)
根據疊代的初值X0,由式(0-1)計算新點集Pi為:
(0-3)
式中,P表示原始未修改過的點集,Pi的下標i表示疊代次數,參數向量X的初始值X0為 。
根據以上數據處理方法,ICP配準算法可以概括為以下七個步驟:
1) 根據點集Plk中的點坐標,在曲面S上搜尋相應最近點點集Prk;
2) 計算兩個點集的重心位置坐標,並進行點集中心化生成新的點集;
3) 由新的點集計算正定矩陣N,並計算N的最大特徵值及其最大特徵向量;
4) 由於最大特徵向量等價於殘差平方和最小時的鏇轉四元數,將四元數轉換為鏇轉矩陣R;
5) 在鏇轉矩陣R被確定後,由平移向量t僅僅是兩個點集的重心差異,可以通過兩個坐標系中的重心點和鏇轉矩陣確定;
6) 根據式(0-3),由點集Plk計算鏇轉後的點集P’lk。通過Plk與P’lk計算距離平方和值為fk+1。以連續兩次距離平方和之差絕對值 作為疊代判斷數值;
7) 當 時,ICP配準算法就停止疊代,否則重複1至6步,直到滿足條件 後停止疊代。
經典算法
ICP算法有較多的數學公式和概念,數學公式總歸看起來費勁,這裡只簡要的理解下其算法步驟:
兩個點集P1,P2,每一步疊代,都朝著距離最小的目標進行。
a.篩選點對:由P1中的點,在P2中搜尋出其最近的點,組成一個點對;找出兩個點集中所有的點對。點對集合相當於進行有效計算的兩個新點集。
b.根據點集對,即兩個新點集,計算兩個重心。
c.由新點集,計算出下一步計算的鏇轉矩陣R,和平移矩陣t(其實來源於重心的差異)。
d.得到鏇轉矩陣和平移矩陣Rt,就可以計算點集P2進行剛體變換之後的新點集P2`,由計算P2到P2`的距離平方和,以連續兩次距離平方和之差絕對值,作為是否收斂的依據。若小於閾值,就收斂,停止疊代。
e.重複a-e,直到收斂或達到既定的疊代次數。
--其中,計算鏇轉矩陣R時,需要矩陣方面的運算。
由新的點集,每個點到重心的距離關係,計算正定矩陣N,並計算N的最大特徵值及其最大特徵向量;其特徵向量等價於鏇轉的四元數(且是殘差和最小的鏇轉四元數),將四元數就可以轉換為鏇轉矩陣。
搜尋方法
1. Point to Point最近點搜尋法
 ICP最近點搜尋圖
ICP最近點搜尋圖Point to Point最近點搜尋法是ICP算法中最經典的一種方法。 Point to Point法根據源曲面上的一個點p,在目標曲面上找出對應於P點距離最近的q點。在這個方法中通常運用kd-tree的方法實現最近點搜尋。如圖1b所示,pi是源曲麵點雲數據中的一個點,Vi是生成目標曲麵點雲數據中距Pi最近的點。根據Vi點搜尋出在曲面上與Vi點相鄰的點構成的三角形格網,計算pi點投影到每個三角形平面上的投影點qi的坐標。對於每個三角形來說,當投影點qi位於三角形內部,則距離最近點是搜尋的最近點,當投影點qi位於三角形外部,搜尋的最近點應位於三角形的兩條邊界上,Vi是該三角形到pi點的最近距離點。將每個三角形確定的最近距離點進行比較可獲得一個最近點。
2. Point to Plane最近點搜尋算法
Point to Plane法是根據源曲面上的一個點p,在目標曲面上找出對應於p點一個最近的q點。搜尋算法是根據源曲面上p點的切平面的法線,確定發現於目標曲面的交點q’。根據目標曲面上q’點求出的過q’點切平面,然後求源曲面上p點到過q’點切平面的垂線的交點q。
3. Point to Projection最近點搜尋算法
Point to Projection最近點搜尋法是一種快速的配準方法,Oq是掃描目標曲面的透視點的位置。Point to Projection法是根據源曲面上的一個點p和透視點Oq,在目標曲面上找出q點作為對應於p點的最近點。通過確定Oq點向p點方向的投影線與目標曲面的交點q,作為搜尋的最近點。

