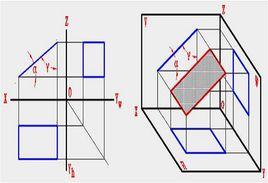
投影面垂直面簡介
垂直於一個投影面而與其他兩投影面傾斜的平面稱為投影面垂直面。垂直於H面的平面稱為鉛垂面,垂直於V面的平面稱為正垂面,垂直於W面的平面稱為側垂面。
對於投影面垂直面,畫圖時,一般先畫積聚性投影(斜線)。讀圖時,如果平面形有一個投影積聚成一條傾斜於投影軸的斜線,則此平面為投影面垂直面;垂直於斜線所在的那個投影面。
鉛垂面
任何物件如鉛垂一樣的與地成正垂直,就是鉛垂方向,與水平面成正交的面,與正面和側面傾斜的平面,就是鉛垂面。
是指和水平面垂直的平面也就是鉛垂線所處的平面。
側垂面
垂直於側面(W面)並與H、V面傾斜的平面稱為側垂面。
垂直於一個投影面而與其他兩投影面傾斜的平面稱為投影面垂直面。垂直於H面的平面稱為鉛垂面,垂直於V面的平面稱為正垂面,垂直於W面的平面稱為側垂面。
對於投影面垂直面,畫圖時,一般先畫積聚性投影(斜線)。讀圖時,如果平面形有一個投影積聚成一條傾斜於投影軸的斜線,則此平面為投影面垂直面;垂直於斜線所在的那個投影面。
相關研究與套用
在建築物的太陽能利用中常涉及鉛垂面上太陽輻射量的計算問題,其理論計算方法中,Perez模型計算較準確但是較繁雜,Hay模型較為簡明實用。在工程套用中,通過計算鉛垂面上日平均輻射量而計算月總輻射量,其中Hay模型較準確 。
在數據挖掘和機器學習的基於距離的各種技術中,例如基於距離的聚類和基於距離的分類,如何度量數據間的相似性已經成為一項基礎任務。對於某一具體問題,採用合適的相似性度量,會使問題得到更有效的解決。
越來越多的研究表明,通過對成對約束(正約束和負約束)的充分利用,從而得到與問題相匹配的相似性度量,能夠大幅度地提升算法性能。
基於約束的相似性度量研究主要是基於約束的距離度量學習,通過對約束信息的利用,學習一個距離度量矩陣,然後再進行分類或者聚類.通過對成對約束尤其是負約束的挖掘,提出一種基於成對約束的相似性度量準則,然後將此準則套用於聚類和分類任務中,分別提出聚類和分類算法,最後在大量標準數據集上將這些算法的性能與流行的算法進行實驗比較,並據此得出了一些經驗性的啟示 。