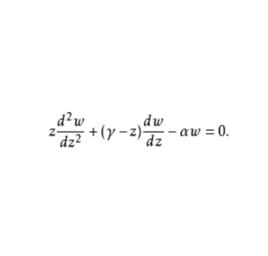簡介
匯合型超幾何方程(confluent hypergeometric equation)，亦稱庫默爾方程（Kummer's equation），是常見的一種匯合型常微分方程，標準形式為
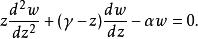匯合型超幾何方程
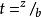匯合型超幾何方程
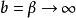匯合型超幾何方程在超幾何方程中作代換，並令(其結果是使超幾何方程的兩個奇點 t=1 及∞“匯合”)即得。合流型超幾何方程有兩個奇點，0和∞；前者為正則奇點，後者為非正則奇點。
德國數學家庫默爾
庫默爾在數論、幾何學、函式論、數學分析、方程論等方面都有較大的貢獻，但最主要的是在函式論、數論和幾何三個方面。
在函式論方面。他研究了超幾何級數，首次對這些級數的單值群的代換進行計算。他發明的級數變換法是相當有名的，在級數的數值計算中有廣泛的套用。
在幾何方面。他研究了一般射線系統，並用純代數方法構作了一個四次曲面，它有16個孤立的二重點，16個奇異切平面，稱之為庫默爾曲面。
在數論方面。庫默爾花的時間最多，貢獻也最大。他研究過高斯（Gauss，Carl Friedrich，1777.4.30-1855.2.23）研究過的高次互反律，研究了數論中最困難的問題之一—費馬大定理，創立了甚至比定理本身更重要的理想數理論。這不僅使得他的證明工作取得了空前的進展（除p=37、59、67外，證明了費馬大定理當p﹤100時都成立），而且為代數學、函式論、方程論等學科提供了一個新的有效工具。這項成果因此而獲得巴黎科學院獎金。在庫默爾理想數理論的基礎上，戴德金（Dedekind，Julius Wilhelm Richard Dedekind，1831.10.6-1916.2.12）創立了一般理想理論。庫默爾的學說經戴德金和克羅內克（Kronecker，Leopold，1823.12.7-1891.12.29）的研究加以發展，建立了現代的代數數理論。
庫默爾還是一個優秀的教師。一直熱心教師之職將近20年。培養了不少數學家，其中最著名的有L.克羅內克、H.A.施瓦茨（Hermann Amandus Schwarz，1843.1.25-1921.11.30）、P.A.哥爾丹（Gordan，Paul Albert，1837.4.27-1912.12.21）等。
庫默爾全集在1975年才由施普林格出版社出版，由著名數學家A.韋伊（Weil，Andre,1906.5.6-1998.8.6）編輯，共兩卷。韋伊在全集導言中說：“即使100年後，細心的讀者仍會從中獲得可觀的教益”。
匯合型超幾何函式
匯合型超幾何方程的基本解即匯合型超幾何函式，即函式
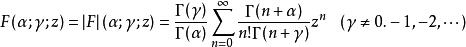匯合型超幾何方程
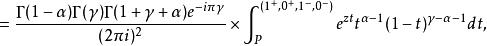匯合型超幾何方程
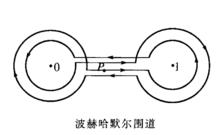匯合型超幾何方程
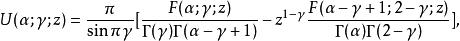匯合型超幾何方程其中的積分路線稱為波赫哈默爾圍道（見右圖），起點P在實軸上，arg t =arg(1-t)=0，分別繞 t=1 和 t=0 正向一周后，再分別繞 t=1和 t=0 逆向一周，最後回到P點。
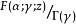匯合型超幾何方程
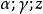匯合型超幾何方程是的單值解析函式。
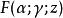匯合型超幾何方程亦稱庫默爾函式。
