概念和遊戲規則
歐氏對局是基於輾轉相除法的一個數學遊戲,其規則如下:對局雙方各自寫一個自然數,猜拳以絕對誰先手,先手者從較大的數扣去較小數的任意倍數,但是要保證差為正,將差和小數組成新的數對,後手以此重複,兩人輪流對局,最先得到含有零的數對者為勝者。比如甲和乙寫的兩個數為75和32,甲是先手,那么其對決過程可以是下面幾個:
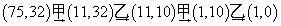 |
| 歐氏對局第一種做法 |
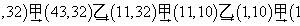 |
| 歐氏對局第二種做法 |
對於數對(m,n),其中m≤n,若n≥2m,那么拿到該數對的人,走法就有多種選擇。我們稱這樣的數對為活絡數對。
反之,若m≤n≤2m,拿到該數對的人只有一條路可走:(m,n)→(m,n-m)。我們稱這樣的數對為死板數對。
費氏數對的歐氏對局
為了研究一般性的歐氏對局,我們先考慮一種特殊情況,那就是費氏數對——以菲波拉契數列的相鄰兩個數為元素的數對。下面的步驟顯示,費氏數對的歐氏對局,其每一步都是死板對局Fn+2=Fn+1+Fn
Fn+1=Fn+Fn-1
Fn=Fn-1+Fn-2
……………………
F4=F3+F2
F3=F2。
每一步都只能到達費氏數列的下一個數對,所以費氏數列的歐氏對局是一個死板對局,這種情況的勝負最簡單。考慮數對(Fn,Fn+1),由於不存在活絡數對,所以計算gcd(Fn,Fn+1)——這兩個數的最大公約數——的步數就是歐氏對局所需要的步數。而我們可以證明,若設E(a,b)為利用輾轉相除法計算a和b最大公約數的步數。那么E(Fn,Fn+1)=n
在這裡我們就從F1開始考慮。所以我們有:E(1,2)=1,E(2,3)=2,E(3,5)=3,E(5,8)=4,E(8,13)=5,…………似乎對於這個沒有什麼可以探究的地方,不過若是在實際操作中,就算告訴你其中的兩個數,那么你必須得用菲波拉契數列的通項公式去判斷他是第幾項,這未免太麻煩,那么有沒有更簡單的辦法?
我們注意到在費氏數列中的算法步驟是間隔、輪流的。這讓我們想起費氏數列的性質,那就是其前後兩項的比值是忽大忽小交叉著靠近黃金分割比的,也就是有下面的性質:
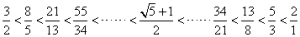 |
| 費氏數對的歐氏對局 |
以黃金分割比γ為分界線,左邊的分子分母就構成我們算法步驟為偶數的數對,右邊就是分子分母構成算法步驟為奇數的數對。而神奇的黃金分割比,就是決定奇偶性的分界線!總結起來就有下面的定理成立:
性質1:設m和n是費氏數列里的相鄰兩項,且m<n,則
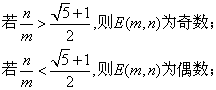 |
| 費氏數對的歐氏對局 |
類費氏數對的歐氏對局
考慮數對(m,n),m≤n≤2m,並且在歐氏對局中,所有的數對都是死板數對,那么其對局過程就是下面:(m,n)→(m,n-m)→(n-m,2m-n)→(2m-n,2n-3m)→(2n-3m,5m-3n)→(5m-3n,5n-8m)→……
我們發現,整個過程其實是下面數列的相鄰兩項組成的數對:
n,m,n-m,2m-n,2n-3m,5m-3n,5n-8m,…………
這是什麼數列?聰明的朋友應該已經看出來了,這就是類斐氏數列!前兩項之和等於後面一項,只不過我們順序顛倒,將大的寫在前面,小的寫在後面而已!比如5m-3n+5n-8m=2n-3m。而且其前兩項必然是0和a的形式,因為只有這樣遊戲才會結束。這似乎就已經提供了與我們前面文章提到的費氏數對相同的處理思路。看來我們有必要對上文中的性質1進行推廣:
類費氏數對的算法步數:
現在有類費氏數列{Fn}:F1=a,F2=ka,Fn+2=Fn+1+Fn.其中k為正整數且k>2。比如1,3,4,7,11,18,……則:
E(Fn,Fn+1)=n
證明:首項數對(Fn,Fn+1)除了最後一步外都是死板的,不過這時候卻已經沒有必要,因為這時候掌握此數對的人可以一步到位拿到零,使之獲勝。我們寫出數對(Fn,Fn+1)的歐氏對局過程:
Fn+1=Fn+Fn-1
Fn=Fn-1+Fn-2
Fn-1=Fn-2+Fn-3
……………………
F3=F2+F1
F2=KF1
很顯然剛好經過n步取到零,雖然最後一步是活絡,但是其持有人已經沒有必要。所以E(Fn,Fn+1)=n。那么我們需要的奇偶性也就出來。因為在我們的歐氏對局中,若整個對局的步數為奇數步,則先入手者為勝;若步數為偶數,則先入手者必敗。這就擁有了和費氏數列一模一樣的處理思想,設類費氏數列為:
F1,F2,F3,F4,F5,F6,…………
E(F1,F2)、E(F3,F4)、E(F5,F6)、E(F7,F8)、E(F9,F10)、…………為奇數。若採用這些數組進行對局,則先入手者必勝。
E(F2,F3)、E(F4,F5)、E(F6,F7)、E(F8,F9)、E(F10,F11)、…………為偶數。若採用這些數組進行對局,則先入手者必敗。
而且幸好,在類費氏數列里擁有著和費氏數列相同的性質,包括:
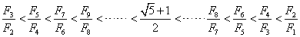 |
| 類費氏數對的歐氏對局 |
這個性質非常重要,因為他給出了和前面判斷斐氏數對的算法步數一模一樣的方法:
性質2:若m和n為類費氏數列的相鄰兩項,並且m<n,則:
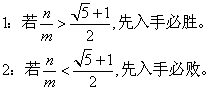 |
| 類費氏數列的歐氏對局 |
歐氏對局的最終解決
這個結論非常重要,雖然解決的只是死板數對的問題,但是實際上已經解決了全部的問題。假設在對局過程中碰到了活絡數對(m,n),即n>2m.這裡假設那么該數對的持有人就可以選擇這樣一條道路:讓餘數大於小數。比如當甲拿到數對(5,21),那么甲可以將之變成(5,16),從而延遲一步,為自己贏取勝利,因為歐氏對局的勝負只不過是一步之差而已。看來,活絡數對就好像是一個活結,持有人可以利用他延遲一步,使得活絡數對的影響消失,最終就相當於類費氏數列的結局。
歐氏對局最終結論:
對於任意的兩個自然數n,m,且n>m,那么:
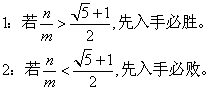 |
| 歐氏對局的最終解決 |
比較詳細點說,當n/m>γ,這時候便進入類斐氏數列第一種情況。如果一直都是死板數對,則先入手者必勝。若是中途出現活絡數對,則持有人可以將之化為情況2,也就是讓接手人得到的數對(m',n')滿足n‘/m’<γ。這是很容易辦到的:
若新的數對(m,n-km)滿足條件m/(n-km)>γ,那么我們可以證明另一個數對(m,n-km+m)滿足條件(n-km+m)/m<γ。也就是先入手著總是可以給對手傳遞一個符合情況2的數對。
這便讓對手陷入失敗的軌道。當然對手也會想方設法將失敗推給你,但是已經沒有辦法。因為若對手接手(m',n')以後一直是死板數對,則根據性質2,其必敗無疑,即使出現活絡,他也不可能傳遞出一對符合情況2的數對。我們可以用不等式證明:
若n<γm,則n-km<γm-km,即m/(n-km)>1/(γ-k)>1/(γ-1)=γ。也就是他傳出來的新數對(m,n-km)不管取什麼k值,都是大於黃金分割比的。所以這種情況下,上面的討論其實已經涉及到了第二種情況。
歐氏對局的遊戲竅門
如果一開始的兩個數就是情況2,但你又是先手,那你就認命吧!如果是第一種情況而你又是先手,那么你第一步至關重要,你必須傳遞出一對符合情況2的數對給對方,才能保證你穩操勝券!任意實數對的歐氏對局
如果我們將思路擴展一下,最先的數不限制在自然數,而是一切實數的話,結果會怎樣?我們要注意的是,對於任意的兩個實數,按照歐氏對局的規則不一定就會出現零,比如
π,3,π-3,6-π,9-2π,5π-12,……
但是也有可能出現零,比如1.5和2.3
2.3,1.5,0.8,0.7,0.1,0.6,0.5,0.4,0.1,0.3,0.2,0.1,0.1,0
再比如1/3和1/5
1/3,1/5,2/15,1/15,1/15,0
實際上我們可以看到,如果n和m都是有理數的話,最終會出現零,因為將兩個有理數化為同分母的分數以後,最終相減的只是分子在相減,實際上也就相當於兩個自然數的情況。但是若兩個數是無理數,也有可能出現零,比如√2和2√2,最終就會出現零。假設最終出現的是0和a,其中a為實數,反推回去就會知道,不可能出現無理數,也就是無理數的最終結果一定是無理數。如果a為無理數,則最初的數對只可能是(ka,ha)其中k和h均為整數的形式,換句話說,只要n/m是一個有理數,那最終結果就可以分出勝負。那么這種情況下的勝負情況又是如何?是否和自然數的勝負情況一樣的呢?
1:假設n和m均為有理數,將他們化成同分母的分數m=g/p,n=h/p。我們可以看到,最終的操作其實只是在分子上進行,所以結果的勝敗也就是等同於g和h,而g/h=m/n,所以我們可以看到,這種情況仍然滿足結論。
2:如果n和m都是無理數,並且n/m是有理數,那么可以令n=pa,m=qa,其中a為一個無理數,所以實際上後面的進行過程都只是在p和q之間進行,因為a一直都被帶著走,而p/q=n/m,所以可以說在這種情況下,仍然滿足歐氏對局的結論。
實際上上面所有的討論過程可以歸結為:數對(m,n)的勝敗與(am,an)的勝敗是一樣的,因為每一步你都可以把公因式帶著走。這也符合我們的結論,即勝敗只取決於這兩個數的比值。以一個例子說明吧:
(1/3a,0.5a)=(2/6a,3/6a)→(2/6a,1/6a)→(1/6a,1/6a)→(0,1/6a)
大家可以看到,實際上整個過程就是數對(1,2)的對局過程,而對於1/6a至始至終都跟著走的。不管a是整數有理數還是實數,甚至於是一個多項式,都是一樣的道理,所以對於實數對(n,m)的歐氏對局,我們依然有下面的結論:
1:若n/m不是有理數,則這樣的歐氏對局不可能會有結果。
2:若n=m,則先手為勝。
3:若n≠m,n>m,且n/m為有理數,則:
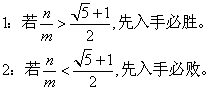 |
| 任意實數對的歐氏對局 |
