什麼樣的問題將是特別重要的定理在下面的表格的方
AH² = BH ·HC
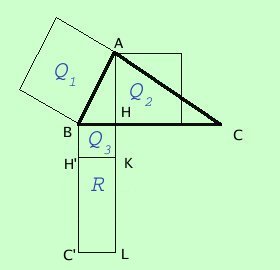
| 假設 BAC三角形 | 論文Q相當於ŕ |
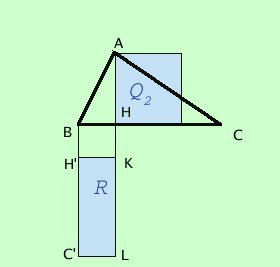
1.Q1=Q3+R
2.Q1=Q2+Q3
3Q3+R=Q2+Q3
4 3雙方同時去掉一個相同的Q3得出R=Q2
歐幾里德在《幾何原本》第九卷,問題20給出如下證明:
設a,b,c,…,k是素數,那么它們的乘積再加1,即abc…k+1或者是素數或者不是素數,
(1)如果abc…k+1是素數,則又多了一個素數;
(2)如果abc…k+1不是素數,則它有一個素因子p,那么p不同於a,b,c,…,k中的任一個。因為若p是a,b,c,…,k其中之一,則p整除abc…k,於是p整除1,這是不可能的
所以無論在那種情況都可以得到一個新的素數,則素數是無限的。
