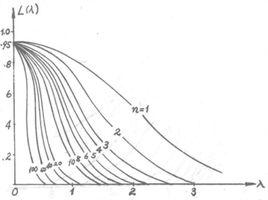
基本介紹
為了分析檢驗結果所可能犯的錯誤,A.Wald引進了所謂效函式(Power function)的概念。記
P(θ)=當參數θ為真時拒絕假設H的機率
=P{拒絕假設H/θ} (1)
上式中,θ可以取不同於θ及θ的其他參數值。常稱P(θ)為檢驗的效函式。
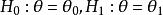 檢驗工作特徵
檢驗工作特徵對於互相競擇的假設來說(記),我們有
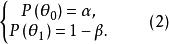 檢驗工作特徵
檢驗工作特徵在實用上,往往以1-P(θ)作為檢驗中所犯錯誤的一種度量,稱它為 檢驗的特性函式或 OC-函式(Operating Characteristic function),常記作L(θ) 。於是:
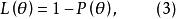 檢驗工作特徵
檢驗工作特徵且
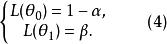 檢驗工作特徵
檢驗工作特徵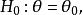 檢驗工作特徵
檢驗工作特徵L(θ)表示了當參數θ為真時採納假設H的機率。對於簡單假設理想的OC-函式具有下列表達形式:
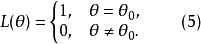 檢驗工作特徵
檢驗工作特徵它的圖形如圖1所示。
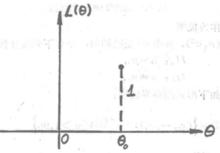 圖1 理想的OC-函式圖示
圖1 理想的OC-函式圖示 檢驗工作特徵
檢驗工作特徵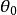 檢驗工作特徵
檢驗工作特徵表達式(5)說明了。當H為正確時,採納它的機率為1,當H為不正確的假設時,採納它的機率為0。但是,我們知道,這種理論的OC-函式在實際檢驗過程中是難於實現的(除非子樣的容量為)。雖然如此,我們可以在假設檢驗的過程中,將實際的OC-函式和理想的OC-函式進行比較,從而作出關於檢驗好壞的某種評定。從上圖可以看出,如果OC-函式所表示的曲線在近傍變化較陡,那么,所對應的檢驗也就越好。
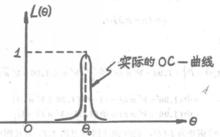 圖2 實際的OC-曲線越近似於理想的OC-曲線,則檢驗有較好的性能
圖2 實際的OC-曲線越近似於理想的OC-曲線,則檢驗有較好的性能對於複合假設
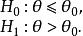 檢驗工作特徵
檢驗工作特徵理想的OC-曲線如下圖所示 。
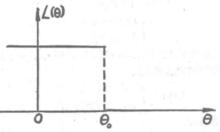 圖3 理想的OC-函式圖示
圖3 理想的OC-函式圖示舉例分析
下面舉一些例子作為說明。
 檢驗工作特徵
檢驗工作特徵 檢驗工作特徵
檢驗工作特徵例1 設,其中是巳知的,今有下列統計假設
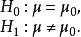 檢驗工作特徵
檢驗工作特徵在5%的水平下,取如下形式的臨界區域。
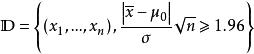 檢驗工作特徵
檢驗工作特徵試確定出檢驗的OC-函式。
解: 由OC-函式的定義,知
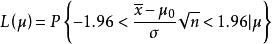 檢驗工作特徵
檢驗工作特徵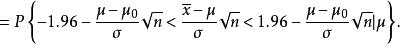 檢驗工作特徵
檢驗工作特徵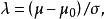 檢驗工作特徵
檢驗工作特徵記,
那么,我們有
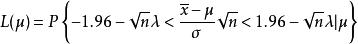 檢驗工作特徵
檢驗工作特徵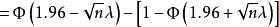 檢驗工作特徵
檢驗工作特徵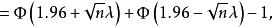 檢驗工作特徵
檢驗工作特徵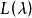 檢驗工作特徵
檢驗工作特徵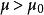 檢驗工作特徵
檢驗工作特徵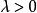 檢驗工作特徵
檢驗工作特徵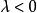 檢驗工作特徵
檢驗工作特徵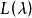 檢驗工作特徵
檢驗工作特徵 檢驗工作特徵
檢驗工作特徵記上述OC函式為,它的曲線圖示見圖4。在該圖中,只製作了即時的OC曲線,當時,由於為的偶函式,故圖形與縱軸對稱。
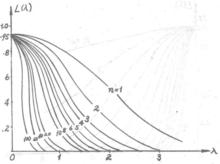 圖4 OC-函式圖示
圖4 OC-函式圖示由圖4看出,當試驗次數n越大時, 曲線越陡,λ越大時,(即參數的真實值μ和μ的差別越大時) OC-函式的值越小。 在圖4中,如果取β=0.05, 則當n=3時,λ≌2.1,此時lμ-μl=2.1σ。因此如果以距離μ為2.1σ的那種參數作為假設H時,犯第二種錯誤的機率為5%,還可以看出,當子樣的容量n>50時,OC-函式所表示的曲線其陡度並沒有顯著的改變。因此假設檢驗中犯兩種錯誤的機率並沒有多大的減少。因此考慮到試驗的費用或試驗條件的限制等等因素時,可以選定適當的試驗次數。OC-曲線有助於試驗設計中的參考。