定義
在正交曲線坐標系中,橢球坐標系具有一定的普遍性,其他可分離變數的十種正交曲線坐標系都是它的特殊情況。由於橢球坐標系所得出之解的普遍性,使它可以直接變換至其他一些正交曲線坐標系中。因此,我們首先討論這種坐標系。
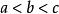 橢球坐標系
橢球坐標系假定實常數 ,則方程
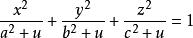 橢球坐標系
橢球坐標系表示一個二次共焦曲面,曲面的大小形狀與u有關。u在不同區間內變化時,它表示不同大小形狀的共焦曲面。為此。我們可按u在不同區間的變化來考查曲面的大小形狀。
(1)當u=0時,則
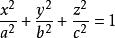 橢球坐標系
橢球坐標系表示橢球面,其半主軸長度為a,b和c。
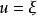 橢球坐標系
橢球坐標系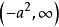 橢球坐標系
橢球坐標系(2)當 在區間 變化時,則
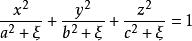 橢球坐標系
橢球坐標系表示共焦橢球坐標系。因為u在該區間內有
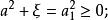 橢球坐標系
橢球坐標系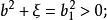 橢球坐標系
橢球坐標系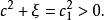 橢球坐標系
橢球坐標系故方程
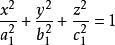 橢球坐標系
橢球坐標系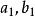 橢球坐標系
橢球坐標系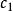 橢球坐標系
橢球坐標系具有橢球面方程的形式, 和 表示變化的半主軸長度,半主軸的變化就形成一系列共焦橢球曲面,如圖1所示。
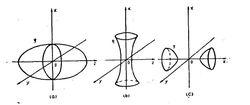 圖1:橢球坐標系的二次共焦曲面
圖1:橢球坐標系的二次共焦曲面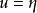 橢球坐標系
橢球坐標系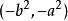 橢球坐標系
橢球坐標系(3)當 在區間 變化時,則
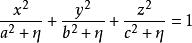 橢球坐標系
橢球坐標系表示共焦單葉雙曲面坐標系.因為u在該區間內有
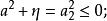 橢球坐標系
橢球坐標系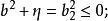 橢球坐標系
橢球坐標系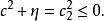 橢球坐標系
橢球坐標系故方程
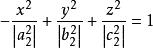 橢球坐標系
橢球坐標系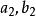 橢球坐標系
橢球坐標系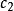 橢球坐標系
橢球坐標系具有單葉雙曲面方程的形式, 和 表示變化的半主軸長度,半主軸的變化就形成一系列共焦單葉雙曲面,如圖1(b)所示。
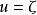 橢球坐標系
橢球坐標系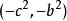 橢球坐標系
橢球坐標系(4)當 在區間 變化時,則
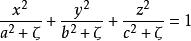 橢球坐標系
橢球坐標系表示共焦雙葉雙曲面坐標系。因為u在該區間內有
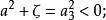 橢球坐標系
橢球坐標系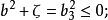 橢球坐標系
橢球坐標系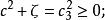 橢球坐標系
橢球坐標系故方程
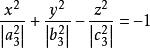 橢球坐標系
橢球坐標系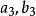 橢球坐標系
橢球坐標系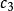 橢球坐標系
橢球坐標系具有雙葉雙曲面方程的形式,和表示變化的半主軸長度,半主軸的變化就形成一系列共焦雙葉雙曲面,如圖1(c)所示。
橢球坐標系與直角坐標系的關係
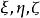 橢球坐標系
橢球坐標系已知u在的相應區間內變化時所分別代表的三種曲面就是橢球坐標系中的三個坐標曲面,即橢球曲面、單葉雙曲面和雙葉雙曲面。然而,我們最常用,最熟悉的是直角坐標系,如能建立這兩種坐標系之間的對應關係.就會給橢球坐標系中的計算帶來方便。
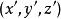 橢球坐標系
橢球坐標系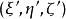 橢球坐標系
橢球坐標系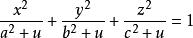 橢球坐標系
橢球坐標系設空間任一點P在直角坐標系中的位置為,代入上述三種坐標系方程中,可求得P在橢球坐標系中的相應位置為。方程可改寫為u的函式形式
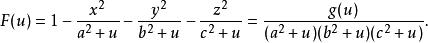 橢球坐標系
橢球坐標系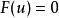 橢球坐標系
橢球坐標系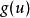 橢球坐標系
橢球坐標系顯然,對於方程,為一三次多項式
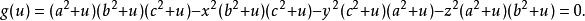 橢球坐標系
橢球坐標系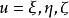 橢球坐標系
橢球坐標系因此,表示方程F(u)=0的三個根,可得
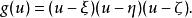 橢球坐標系
橢球坐標系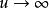 橢球坐標系
橢球坐標系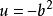 橢球坐標系
橢球坐標系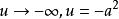 橢球坐標系
橢球坐標系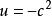 橢球坐標系
橢球坐標系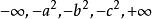 橢球坐標系
橢球坐標系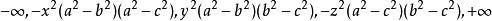 橢球坐標系
橢球坐標系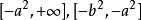 橢球坐標系
橢球坐標系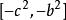 橢球坐標系
橢球坐標系由上述F(u)的方程知,當或時g(u)為正值;當,或時,g(u)為負值。如圖2所示.當u沿u軸依次取值時,g(u)則按上述三項多項式依次取值。由此可見,F(u)或g(u)的三個根是互不相等的實根,分別位於區間和中.可寫為
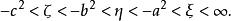 橢球坐標系
橢球坐標系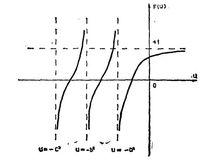 圖2:函式F(u)的變化曲線
圖2:函式F(u)的變化曲線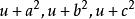 橢球坐標系
橢球坐標系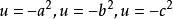 橢球坐標系
橢球坐標系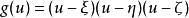 橢球坐標系
橢球坐標系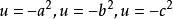 橢球坐標系
橢球坐標系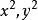 橢球坐標系
橢球坐標系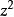 橢球坐標系
橢球坐標系在上述F(u)方程中,依次乘以,並依次令.再代入式;或者在上述g(u)兩式中,依次令,均可求得和的表達式.開方之後寫為
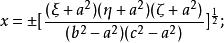 橢球坐標系
橢球坐標系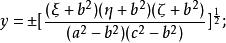 橢球坐標系
橢球坐標系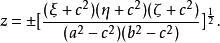 橢球坐標系
橢球坐標系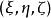 橢球坐標系
橢球坐標系以上三式建立了橢球坐標系與直角坐標系(x,y,z)之間非單值的對應關係。
