定義
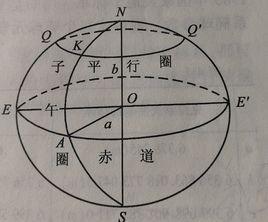
為了解決在大地水準面這個複雜曲面上進行數據處理的困難問題,在測繪工作中常選用一個表面非常接近大地水準面、並且可以用數學模型表達的幾何形體來代替地球的幾何形狀 ,此幾何形體通常稱為地球橢球體,又稱旋轉橢球體。
 旋轉橢球體的形狀
旋轉橢球體的形狀地球橢球是控制測量中用以代表地球的橢球,通常簡稱橢球,它是地球的數學代表。地球橢球體形狀及大小通常由子午橢圓的五個基本幾何參數(或稱元素)來決定,包括橢圓的長半軸a,短半軸b,橢圓扁率、橢圓的第一偏心率和第二偏心率。其中橢球的扁率公式為
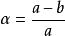 橢球扁率
橢球扁率性質
扁率α反映了橢球體的扁平程度。當a=b時,α=0,此時橢球體變為球體;當b減小時,α增大,則此時橢球體變扁;當b=0時,α=1,則變為平面。因此,扁率的大小由橢球的長半軸與短半軸共同決定,且其值介於1和0之間。
當把地球看作圓球時,地球大氣呈球對稱分布,大氣折射中心與地球的球心重合;而當考慮橢球扁率影響時,折射中心相對於地球橢球中心有了偏移。為了改正由於扁率帶來的偏差,折射角與影響參數的計算應該相對於折射中心。 因此,橢球扁率對各項研究帶來的誤差等影響,是不容忽視的。
套用
傳統大地測量利用天文大地測量和重力測量資料推求地球橢球的幾何參數。從19世紀以來,已經求出許多地球橢球參數。 較著名的有:①克拉索夫斯基橢球體,其扁率規定為1/298.3;②1975年國際橢球體,規定扁率為1/298.257;③WGS-84橢球體,規定扁率為1/298.257223563;④2000中國大地坐標系(CGCS2000),規定其為1/298.257222101。
在地質歷史上的變化下限
利用地球扁率,將地球假設為彈性橢球體,根據彈性動力學理論推導出扁率下限公式。扁率與地球平均密度、引力加速度、自轉角速度、平均半徑、彈性模量等均相關。根據地質歷史時期半徑、質量、角速度等變化值可計算出各地質歷史時期的橢球扁率值 ,從而作為扁率變化值的下限,用以研究地球形狀的長期變化。
子午線弧長公式簡化
子午線弧長計算是經典大地測量問題之一,因子午線弧長問題涉及橢圓積分,不能直接求出,其經典算法是按二項式定理展開的級數展開。為提高收斂速度,國際上多以橢球的扁率來進行代換。利用橢球扁率進行對子午線弧長公式的簡化,豐富了子午線弧長的理論與套用。
對引潮力位的影響
固體潮廣泛用於地球物理、空間科學與地震監測研究,而引潮力位(TGP)調和展開是固體潮研究與分析計算中的基本理論問題,也是潮汐觀測分析與研究工作的基礎 。關於TGP調和展開,有頻譜分析法與解析演繹法,其展開精度已能滿足重力觀測和空間測地技術的需要,但根據位理論與微積分方法,還可導出顧及地球扁率的TGP表達式。從引力潮位出發,通過對外界天體在地球質心處產生引力、進行受力分析的研究,並基於空間直角坐標系轉換方法,可推導出橢球扁率對TGP的表達式,從而產生對引力潮位的重新討論。