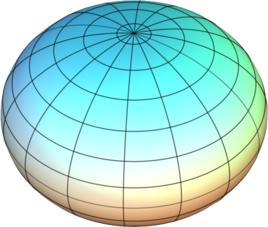
橢球
橢球是一種二次曲面,是橢圓在三維空間的推廣。橢球在 xyz-笛卡兒坐標系中的方程是:
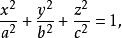 參考橢球
參考橢球其中a和b是赤道半徑(沿著x和y軸),c是極半徑(沿著z軸)。這三個數都是固定的正實數,決定了橢球的形狀。
如果三個半徑都是相等的,那么就是一個球;如果有兩個半徑是相等的,則是一個類球面。點(a,0,0)、(0,b,0)和(0,0,c)都在曲面上。從原點到這三個點的線段,稱為橢球的 半主軸。它們與橢圓的半長軸和半短軸相對應。
橢球的性質
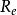 參考橢球
參考橢球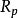 參考橢球
參考橢球記長軸半徑,短軸半徑。常用的地球參考橢球在直角坐標系Oxyz中可表示為:
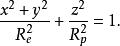 參考橢球
參考橢球長短軸半徑及扁率{\displaystyle f}之間有如下關係:
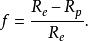 參考橢球
參考橢球有時還會用到偏心率:
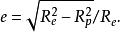 參考橢球
參考橢球第一偏心率:
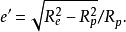 參考橢球
參考橢球第二偏心率:
坐標
參考橢球的主要作用就是作為定義經度、緯度和高程的基礎。
地球參考橢球
最常用的參考橢球,是美國國防部製圖局(DMA)在1984年構建的WGS84。
下表列出了一些最常見的參考橢球:
| 橢球名稱 | 長半軸 (米) | 短半軸 (米) | 扁率的倒數, 1/f | 使用的國家和地區 |
| 克拉克(Clarke)1866 | 6 378 206.4 | 6 356 583.8 | 294.978 698 2 | 北美 |
| 克拉克(Clarke)1880 | 6 378 245 | 6 356 510 | 293.46 | 北美 |
| 白塞爾(Bessel)1841 | 6 377 397.155 | 6 356 078.965 | 299.152 843 4 | 日本及台灣 |
| International 1924 | 6 378 388 | 6 356 911.9 | 296.999 362 1 | 歐洲、北美及中東 |
| 克拉索夫斯基(Krasovsky)1940 | 6 378 245 | 6 356 863 | 298.299 738 1 | 俄羅斯、中國 |
| 1975年國際會議推薦的參考橢球 | 6 378 140 | 6 356 755 | 298.257 | 中國 |
| GRS 1980 | 6 378 137 | 6 356 752.3141 | 298.257 222 101 | |
| WGS 1984 | 6 378 137 | 6 356 752.3142 | 298.257 223 563 | 全球 |
| Sphere(6371 km) | 6 371 000 | 6 371 000 |  參考橢球 參考橢球 |
大陸地區在1954年前曾採用International 1924參考橢球,之後較長一段時間內採用基於克拉索夫斯基(Krasovsky)1940的1954年北京坐標系。1980年開始使用1975年國際大地測量與地球物理聯合會第16屆大會推薦的參考橢球。