有限自動機論
正文
自動機論的次級學科,研究存儲量有限的離散數字系統的功能和結構以及兩者的關係。自動電話交換機、開關網路和計算機等物理系統是存儲量有限的離散數字系統的實例。有限自動機就是這種有限離散數字系統的抽象數學模型。有限自動機論的主要研究課題是分析和綜合問題:給出一個具體的自動機或實現它的邏輯網路,分析有限自動機的功能描述;給出有限自動機的功能描述,綜合出能實現此功能的有限自動機,並由此設計出滿足要求的邏輯網路。具體內容有邏輯網路實現、狀態化簡、狀態分配、神經網路、有限接收機和有限自動機的分解等。
發展簡況 1938年美國科學家C.E.仙農等套用布爾代數對繼電路接點電路進行研究,形成了開關網路理論,為有限自動機論的建立奠定了基礎。電子數字計算機出現以後,由於對計算機進行邏輯設計的需要,開關網路受到人們普遍重視。50年代中期,美國科學家D.A.赫夫曼和E.F.莫爾各自獨立地研究了時序網路理論,形成了有限自動機論的雛形。從此有限自動機論得到深入和系統的研究,已成為自動機論中一個較完整、較成熟的理論。
基本內容 有限自動機也稱時序機。有限自動機的數學定義是:由輸入集合X、輸出集合Y、狀態集合Q、狀態函式δ與輸出函式λ組成的抽象系統M(X,Y,Q,δ,λ),其中 X、Y、Q 都是有限集合,δ和λ分別是Q×X 到 Q 和Q×X到Y上的單值函式。系統對時間來說是離散的,設在某一時刻t時系統處於某狀態q∈Q,如果此時系統的輸入為x∈X,則系統的輸出為y=λ(q,x),且在時刻t+1時,系統的狀態變為q′=δ(q,x)。例如,一個自動機的輸入集合為X={0,1},輸出集合為Y={0,1},狀態集合Q={q0,q1,q2},其δ,λ函式如表1,表中第i行第j列處的內容是δ(qi,j)/λ(qi,j)。
 有限自動機論
有限自動機論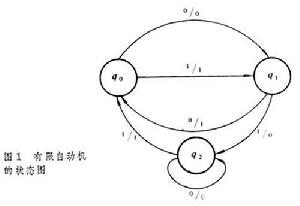 有限自動機論
有限自動機論前面定義的有限自動機,對於所有輸入來說,在給定狀態下都有唯一確定的輸出和下步狀態,因此也稱完全定義的有限自動機,但實際套用中有時也考慮輸出函式δ和狀態函式δ對某些狀態無定義的情形,人們把這種情形下的自動機稱為不完全定義的有限自動機。另外,有時也考慮狀態函式和輸入函式取多值的情形,稱為非確定型有限自動機。為了區別起見,把原定義的有限自動機稱為確定型有限自動機。
邏輯網路 基本的邏輯元件按是否具有記憶功能,可以分為兩類。一類是組合元件,如各種與、或、非門等,這類元件在時刻t的輸入可以完全決定時刻t的輸出。另一類元件是記憶元件,這類元件的輸出不僅取決於元件的輸入,而且取決於元件當前所處的狀態,元件下一時刻的狀態也由輸入和狀態決定。各種觸發器和延遲器等都屬於記憶元件。把一些基本邏輯元件按一定要求連線起來,就組成邏輯網路。如果把邏輯網路中進入記憶元件的輸入線去掉後所得網路不再含有迴路,則稱這樣的網路為合式網路。不含記憶元件的合式網路稱組合網路。
組合網路不含記憶元件,所以網路在時刻t的輸入可以完全決定它在時刻t的輸出。如果組合網路的輸入是x1,…,xk,輸出是y1,…,yn,其功能可由下面方程組描述
yi=f(x1,…,xk) (i=1,2,…,n)
當所有組合元件都是二值元件時,此方程組就是描述組合網路功能的布爾方程組。在研究組合網路的分析與綜合時,採用布爾代數或卡諾圖等方法,把這種布爾方程組化簡,設計出結構簡單而又具有同樣功能的組合網路。一般邏輯網路含有記憶元件,其輸出不僅取決於輸入,而且取決於網路的內部狀態,所以邏輯網路比組合網路複雜。但是,任何合式網路的功能都可以用一個有限自動機來描述;任何一個有限自動機所描述的功能,都可以用合式網路實現。在工程實現上,要求對於一個給定的有限自動機建立起實現此有限自動機的邏輯網路,為使建立的邏輯網路儘可能簡單,人們自然考慮到有限自動機的化簡和狀態賦值等問題。
狀態化簡 在很多實際問題中,要求去掉有限自動機中起同樣作用的狀態,設計出功能相同而狀態最少的系統。這個問題反映在理論上,就是有限自動機的化簡問題。
M1和M2是兩個有限自動機,若它們具有同樣的輸入集合和輸出集合,q1是M1的一個狀態,q2是M2的一個狀態,如果q1和q2對所有的輸入序列都有相同的輸出,則說q1和q2是兩個等價的狀態。這裡M1和M2可以是同一自動機,這時就有一個自動機的兩個狀態等價的概念。如果一個有限自動機的任意兩個等價的狀態必是同一狀態,則說這個有限自動機處於最簡形式。如果對於自動機M1的每一個狀態,總有自動機M2的一個狀態與之等價,反之,對於M2的每一狀態,也總有M1的一個狀態與之等價,則說有限自動機M1與M2等價。兩個狀態等價說明兩個狀態具有同樣的功能,兩個自動機等價說明兩個自動機具有同樣的功能。為使系統儘可能簡單,人們當然對等價的最簡形式的自動機感興趣。有限自動機論已經證明:在同構的意義下,任何有限自動機都有與之等價的最簡形式的有限自動機,並且這種最簡形式的有限自動機是唯一的。根據有限自動機論,對給定有限自動機,可有效地求出與之等價的最簡形式的有限自動機。
對於不完全定義的有限自動機,情形則複雜一些。相當於狀態等價與自動機等價的概念,在不完全定義的有限自動機中有狀態覆蓋和有限自動機覆蓋的概念。其他簡問題就是求覆蓋一個不完全定義的有限自動機的狀態最少的完全定義的有限自動機。
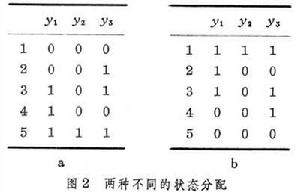
狀態分配 組成實際邏輯網路的基本元件一般是二值元件。要構造具有多個狀態的網路,就要使用多個基本記憶元件,利用這些記憶元件的各種狀態組合來表示不同的狀態。例如,可用3個二值元件y1、y2、y3來表示具有5個狀態的系統,對每一狀態指定一組代表基本元件狀態組合的編碼(圖2a)。
 有限自動機論
有限自動機論對於異步邏輯網路,其狀態分配問題主要是考慮狀態轉換上的穩定性,實現無競爭狀態分配,因而與同步網路的狀態分配有較大的差別。
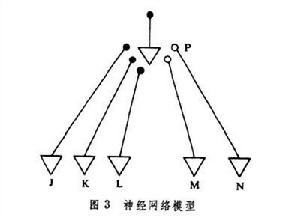
神經網路 1943年W.S.麥克卡洛克和W.比脫斯提出了一個神經系統的模型。根據這個模型,神經系統的基本單位是神經元。每個神經元由細胞體、神經纖維和神經末梢組成,神經纖維是由細胞體發出的一個或數個神經末梢。有限個神經元連線在一起就構成了神經網路。在連線時,任一神經元的任一神經末梢只能同一個細胞體相接觸。每一神經末梢只能有兩種狀態,即興奮狀態和抑止狀態(圖3)。興奮神經末梢用黑點表示,抑止神經末梢用圓圈表示。這種神經網路模型是有限自動機的一個實際例子。S.C.克林尼於1951年在麥克卡洛克和比脫斯神經網路模型的基礎上,提出了正則事件(正則語言)的概念,證明了正則事件是可以被神經網路或有限自動機表示的事件,而且神經網路或有限自動機可表示的事件也一定是正則事件。
 有限自動機論
有限自動機論若有限接收機M處於初始狀態q0,對確定型有限接收機來說,如果對M輸入字元序列x後,M最終達到的狀態屬於 F,則說M能接收字元序列x。對非確定型接收機來說,輸入字元序列x後,M可達到的狀態是依次輸入x中各個元素後所有可能的狀態集合;如果此集合中有一狀態屬於F,則說M能識別字元序列x。非確定型有限接收機和確定型有限接收機都接收同樣一類語言,即正則語言。
參考書目
C.E.申南,J.麥克卡賽編,陳中基編譯:《自動機研究》,科學出版社,北京,1963。(C.E.Shannon and J.McCarthy,Automata Studies,Princeton Univ.Pr.,Princeton,N.J.,1956.)
M. A. Arbib, Theories of Abstract Automata,Prentice Hall, Englewood Cliffs, N.J., 1969.

