定義
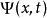機率流
機率流在量子力學裡，從機率守恆可以得到“機率連續性方程”。設定一個量子系統的波函式為。定義機率流 為
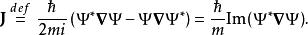機率流
機率流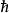
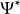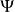機率流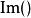
機率流
機率流其中， 是約化普朗克常數，m是質量，是是共軛複數，是取括弧內項目的復值。
機率保守定律
機率流滿足量子力學的連續方程：
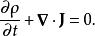機率流
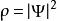機率流其中，是機率密度。
套用高斯公式，等價地以積分方程表示，
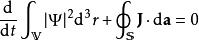機率流；(1)
其中，V是任意三維區域，S 是V的邊界曲面。這就是量子力學 機率守恆定律的方程。
方程 (1) 左邊第一個體積積分項目（不包括對於時間的偏微分），即是測量粒子位置時，粒子在V內的機率。第二個曲面積分是機率流出V的通量。總之，方程 (1) 表明，粒子在三維區域V內的機率對於時間的微分，加上機率流出三維區域V的通量，兩者的總和等於零。
連續方程導引
測量粒子在三維區域V內的機率P是
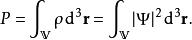機率流機率對於時間的導數是
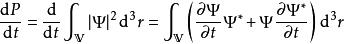機率流；(2)
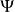機率流假設的含時薛丁格方程為
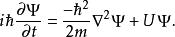機率流
機率流其中，是位勢。
將含時薛丁格方程代入方程 (2) ，可以得到
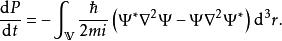機率流套用一則矢量恆等式，可以得到
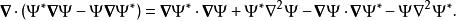機率流這方程右手邊第一個項目與第三個項目互相抵銷，將抵銷後的方程代入，
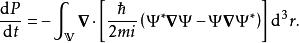機率流將機率密度方程與機率流定義式代入，
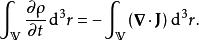機率流這相等式對於任意三維區域V都成立，所以，被積項目在任何位置都必須等於零：
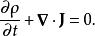機率流範例
平面波
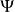機率流設定一個粒子的波函式為三維空間的平面波，
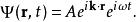機率流
機率流其中，A 是振幅常數，k是波數，r是位置，是角頻率，t是時間。
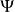機率流的機率流是
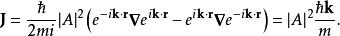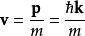機率流
機率流這只是振幅的平方乘以粒子的速度。
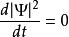機率流請注意，雖然這平面波是定態，在每一個的地點，，但是機率流仍舊不等於0。因此可以推論，雖然機率密度不顯性地跟時間有關，粒子仍可能移動於空間中。
盒中粒子
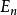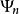機率流
機率流思考一維盒中粒子問題，能級為的本徵波函式是
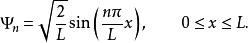機率流其中，L是一維盒子的寬度，兩扇盒壁的位置分別在x=0與 x=L 。
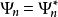機率流由於，其機率流為
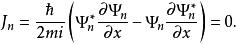機率流相關條目
•階梯位勢
•透射係數
